Bài 6. Ba đường conic
Chương VII. Phương pháp tọa độ trong mặt phẳng
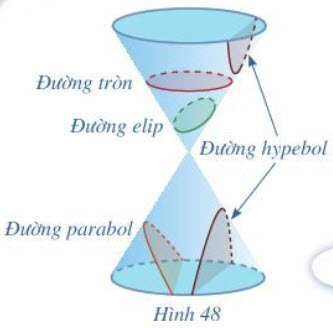
Từ xa xưa, người Hy Lạp đã biết rằng giao tuyến của mặt nón tròn xoay và một mặt phẳng không đi đình của nón là đường tròn hoặc đường cong mà ta gọi là đường conic (Hình 48). Từ "conic" xuất phát từ gốc tiếng Hy Lạp Konos, nghĩa là mặt nón.
Đường conic gồm những loại đường nào và được xác định như thế nào?
1. Đường elip
Định nghĩa đường elip
Cho hai điểm F1 , F2 cố định có khoảng cách F1F2 = 2c (c > 0) (Hình 51).
Đường elip (còn gọi là elip) là tập hợp các điểm M trong mặt phẳng sao cho MF1 + MF2 = 2a, trong đó a là số cho trước lớn hơn c.
Hai điểm F1 và F2 được gọi là hai tiêu điểm của elip.
Phương trình chính tắc của elip
Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho MF1 + MF2 = 2a, ở đó F1F2 = 2c (với a > c > 0). Ta chọn hệ trục tọa độ Oxy có gốc O là trung điểm của F1F2 , trục Oy là đường trung trực của F1F2 và F2 nằm trên tia Ox (Hình 52). Khi đó:
• F1(-c ; 0) và F2(c ; 0) là hai tiêu điểm của elip (E).
• (E) cắt trục Ox tại hai điểm A1(-a ; 0) và A2(a ; 0).
• (E) cắt trục Oy tại hai điểm B1(0 ; -b) và B2(0 ; b) với $b=\sqrt{a^2-c^2}$.
• Phương trình chính tắc của elip (E) là:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}$ = 1, trong đó a > b > 0.
Chú ý: Đối với elip (E) có phương trình nêu ở trên, ta có:
• c2 = a2 - b2 , ở đó 2c = F1F2.
• Nếu M(x ; y) ∈ (E) thì -a ≤ x ≤ a.
Ví dụ
1)
• Quan sát một cốc thủy tinh hình trụ có chứa nước màu:
Nếu đặt cốc nước trên mặt bàn nằm ngang thì mặt thoáng của nước trong cốc là một hình tròn, giới hạn bởi một đường tròn.
Nếu ta nghiêng cốc nước đi thì mặt thoáng của nước được giới hạn bởi một đường elip (Hình 49).
• Nhà thiên văn học người Đức là Johannes Kepler (1571 - 1630) đã chứng tỏ rằng: Mỗi hành tinh trong Hệ Mặt Trời đều chuyển động theo quỹ đạo là một đường elip (Hình 50).
2) Lập phương trình chính tắc của elip (E) đi qua hai điểm M(0 ; 3) và N(3 ; $-\frac{12}{5}$).
Giải
Elip (E) có phương trình chính tắc là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}$ = 1 (với a > b > 0) (1).
M(0 ; 3) ∈ (E) nên $\frac{0^2}{a^2}+\frac{3^2}{b^2}$ = 1 ⇔ b2 = 9.
N(3 ; $-\frac{12}{5}$) ∈ (E) nên $\frac{3^2}{a^2}+\frac{\left(\frac{-12}{5}\right)^2}{9}$ = 1 ⇔ a2 = 25.
Vậy elip (E) có phương trình chính tắc là: $\frac{x^2}{25}+\frac{y^2}{9}$ = 1.
2. Đường Hypebol
Định nghĩa đường hypebol
Cho hai điểm F1 , F2 cố định có khoảng cách F1F2 = 2c (c > 0) (Hình 53).
Đường hypebol (còn gọi là hypebol) là tập hợp các điểm M trong mặt phẳng sao cho |MF1 - MF2| = 2a, trong đó a là số cho trước nhỏ hơn c.
Hai điểm F1 và F2 được gọi là hai tiêu điểm của hypebol.
Phương trình chính tắc của hypebol
Tương tự elip, ta chọn trục Ox là đường thẳng F1F2 , trục Oy là đường trung trực của F1F2 = 2c (c > 0), gốc tọa độ O là trung điểm của F1F2 (Hình 54).
Khi đó, hai tiêu điểm của hypebol là F1(-c ; 0) và F2(c ; 0).
Hypebol (H) có phương trình chính tắc là
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, với a > 0, b > 0.
Chú ý: Đối với hypebol (H) có phương trình nêu ở trên, ta có:
• c2 = a2 + b2 , ở đó 2c = F1F2.
• Nếu M(x ; y) ∈ (H) thì x ≤ -a hoặc x ≥ a.
Ví dụ
1)
Mặt cắt đứng của một tháp cảng được thiết kế có dạng hypebol. Dạng này đòi hỏi ít vật liệu xây dựng hơn những dạng hình khác.
(Nguồn: https://flickr.com)
Mặt cắt đứng của ống khói nhà máy điện hạt nhân được thiết kế có dạng hypebol.
(Nguồn: https://pixabay.com)
2) Viết phương trình hypebol sau đây dưới dạng chính tắc: 4x2 – 9y2 = 1.
Giải
Phương trình chính tắc của hypebol có dạng: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, với a > 0, b > 0.
Ta có: 4x2 – 9y2 = 1 ⇔ $\frac{x^2}{\left(\frac{1}{2}\right)^2}-\frac{y^2}{\left(\frac{1}{3}\right)^2}=1$.
Vậy phương trình chính tắc của hypebol là $\frac{x^2}{\left(\frac{1}{2}\right)^2}-\frac{y^2}{\left(\frac{1}{3}\right)^2}=1$.
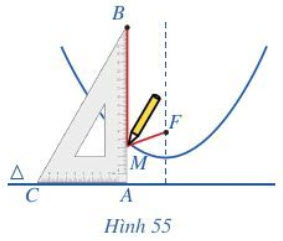
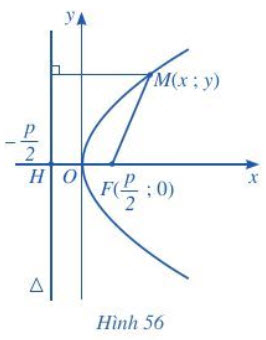
3. Đường Parabol
Định nghĩa đường parabol
Cho một điểm F cố định và một đường thẳng ∆ cố định không đi qua F.
Cho cạnh AC của ê ke trượt trên ∆ (Hình 55). Khi đó, đầu bút chì (điểm M) (ép sát dợi dây màu đỏ có độ dài (l = AB) vào cạnh AB làm căng dây) sẽ vạch nên một đường mà ta gọi là đường parabol.
Khi M thay đổi, ta có: MA = MF.
Đường parabol (còn gọi là parabol) là tập hợp các điểm M trong mặt phẳng cách đều F và ∆.
Điểm F gọi là tiêu điểm của parabol. Đường thẳng ∆ gọi là đường chuẩn của parabol.
Phương trình chính tắc của parabol
Cho parabol (P) với tiêu điểm F và đường chuẩn ∆.
Kẻ FH ⊥ ∆ (H ∈ ∆). Đặt PH = p > 0. Ta chọn hệ trục tọa độ Oxy sao cho gốc O là trung điểm của FH và F nằm trên tia Ox (Hình 56).
• Suy ra: Tiêu điểm ${\color{Blue}F\left(\frac{p}{2};0\right)}$ và phương trình đường chuẩn ∆ là ${\color{Blue}x+\frac{p}{2}=0}$.
• Phương trình chính tắc của parabol (P) là:
y2 = 2px (với p > 0).
Chú ý: Nếu M(x ; y) ∈ (P) thì x ≥ 0.
Ví dụ
1) Đường parapol trong thực tế:
Để giảm lực tác động lên cây cầu người ta thiết kế cầu có dạng hình parabol quay bề lõm xuống phía dưới.
(Nguồn: https://commons.wikimedia.org)
Đài phun nước với các tia nước có dạng hình parabol.
(Nguồn: https://commons.wikimedia.org)
2) Viết phương trình các parabol sau đây dưới dạng chính tắc:
a) $x=\frac{y^2}{4}$; b) x – y2 = 0.
Giải
Phương trình chính tắc của parabol có dạng: y2 = 2px (với p > 0).
a) $x=\frac{y^2}{4}$ ⇔y2 = 2. 2x.
Vậy phương trình chính tắc của parabol là y2 = 2. 2x (với p = 2).
b) x – y2 = 0 ⇔ y2 = 2. $\frac{1}{2}$x.
Vậy phương trình chính tắc của parabol là là y2 = 2. $\frac{1}{2}$x (với p = $\frac{1}{2}$).
Xem thêm các bài học khác :