Bài 4. Ví trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
Chương VII. Phương pháp tọa độ trong mặt phẳng
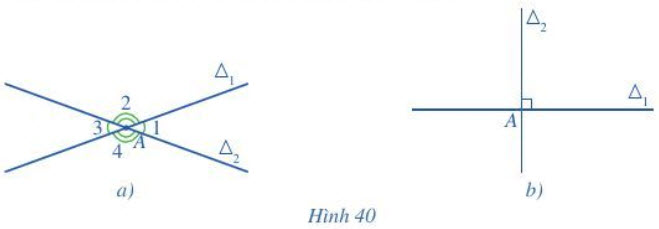
1. Ví trí tương đối của hai đường thẳng
Trong mặt phẳng tọa độ, cho hai đường thẳng ∆1 và ∆2 lần lượt có vectơ chỉ phương là ${\color{Blue}\overrightarrow{u_1},\overrightarrow{u_2}}$. Khi đó:
• ∆1 cắt ∆2 ⇔ ${\color{Blue}\overrightarrow{u_1},\overrightarrow{u_2}}$ không cùng phương.
• ∆1 // ∆2 ⇔ ${\color{Blue}\overrightarrow{u_1},\overrightarrow{u_2}}$ cùng phương và có A ∈ ∆1 nhưng A ∉ ∆2.
• ∆1 ≡ ∆2 ⇔ ${\color{Blue}\overrightarrow{u_1},\overrightarrow{u_2}}$ cùng phương và có A ∈ ∆1 , A ∈ ∆2.
Chú ý:
• ∆1 ⊥ ∆2 ⇔ ${\color{Blue}\overrightarrow{u_1}⊥\overrightarrow{u_2}}$.
• Có thể dựa vào cặp vectơ pháp tuyến của hai đường thẳng để xét vị trí tương đối của chúng.
• Cho ∆1: a1x + b1y + c1 = 0 và ∆2: a2x + b2y + c2 = 0.
Tọa độ giao điểm của ∆1 và ∆2 là nghiệm của hệ phương trình (I): ${\color{Blue}\left\{\begin{matrix}a_1x+b_1y+c_1=0\\a_2x+b_2y+c_2=0.\end{matrix}\right.}$
∆1 cắt ∆2 ⇔ hệ (I) có nghiệm duy nhất (x0 ; y0).
∆1 // ∆2 ⇔ hệ (I) vô nghiệm.
∆1 ≡ ∆2 ⇔ hệ (I) có vô số nghiệm.
Ví dụ
1) Xét vị trí tương đối của hai đường thẳng
$∆_1:\left\{\begin{matrix}x=1+t_1\\y=-2+t_1\end{matrix}\right.$ và $∆_2:\left\{\begin{matrix}x=2t_2\\y=-3+2t_2\end{matrix}\right.$.
Giải
Đường thẳng ∆1, ∆2 lần lượt có vectơ chỉ phương là $\overrightarrow{u_1}=(1;1),\overrightarrow{u_2}=2;2$.
Ta có: $\overrightarrow{u_2}=2\overrightarrow{u_1}$ ⇒ $\overrightarrow{u_1},\overrightarrow{u_2}$ cùng phương.
Chọn t1 = 0, ta được điểm M(1 ; -2) ∈ ∆1. Thay tọa độ điểm (1 ; -2) vào phương trình ∆2, ta được:
$\left\{\begin{matrix}-1=2t_2\\-2=-3+2t_2\end{matrix}\right.⇔\left\{\begin{matrix}t_2=\frac{1}{2}\\t_2=\frac{1}{2}\end{matrix}\right.$
nên điểm M(1 ; -2) ∈ ∆2. Vậy ∆1 trùng với ∆2.
2) Xét vị trí tương đối của hai đường thẳng d: x + 2y – 2 = 0 và Δ: x + 2y + 2 = 0.
Giải
Tọa độ giao điểm của d và ∆ là nghiệm của hệ phương trình:
$\left\{\begin{matrix}x+2y-2=0\\x+2y+2=0\end{matrix}\right.$
Hệ trên vô nghiệm nên d // ∆.
2. Góc giữa hai đường thẳng
♦ Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành bốn góc (Hình 40a).
• Nếu ∆1 và ∆2 không vuông góc nhau thì góc nhọn trong bốn góc tạo thành được gọi là được gọi là góc giữa hai đường thẳng ∆1 và ∆2.
• Nếu ∆1 ⊥ ∆2 (Hình 40b). thì ta nói góc giữa hai đường thẳng ∆1 và ∆2. bằng 90°.
Góc giữa hai đường thẳng ∆1 và ∆2 được kí hiệu là ${\color{Blue}\left(\widehat{∆_1,∆_2}\right)}$ hoặc ${\color{Blue}(∆_1,∆_2)}$.
Quy ước: Khi ∆1 // ∆2 hoặc ∆1 ≡ ∆2 thì (∆1 , ∆2) = 0°.
Nhận xét: (∆1 , ∆2) ≤ 90°.
♦ Trong mặt phẳng tọa độ, cho hai đường thẳng ∆1 và ∆2 có vectơ chỉ phương lần lượt là $\overrightarrow{u_1}=(a_1;b_1),\overrightarrow{u_2}=(a_2;b_2)$. Ta có:
cos(∆1 , ∆2) = $\left|cos(\overrightarrow{u_1},\overrightarrow{u_2})\right|=\frac{|a_1a_2+b_1b_2|}{\sqrt{a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}$.
Nhận xét:
• ∆1 ⊥ ∆2 ⇔ a1a2 + b1b2 = 0.
• Cho hai đường thẳng ∆1 và ∆2 có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1},\overrightarrow{n_2}$. Ta cũng có:
cos(∆1 , ∆2) = $\left|cos(\overrightarrow{n_1},\overrightarrow{n_2})\right|$.
Ví dụ
Tính số đo góc giữa hai đường thẳng ∆1: 2x - y = 0 và ∆2: -x + 3y - 5 = 0.
Giải
∆1 và ∆2 có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}$ = (2 ; -1), $\overrightarrow{n_2}$ = (-1 ; 3). Ta có:
cos(∆1 , ∆2) = $\left|cos(\overrightarrow{n_1},\overrightarrow{n_2})\right|=\frac{|2.(-1)+(-1).3}{\sqrt{2^2+(-1)^2}.\sqrt{(-1)^2+3^2}}=\frac{\sqrt{2}}{2}$
Vậy (∆1, ∆2) = 45°.
3. Khoảng cách từ một điểm đến một đường thẳng
Trong mặt phẳng tọa độ, cho đường thẳng ∆ có phương trình ax + by + c = 0 (a2 + b2 > 0) và điểm M(x0 ; y0). Khoảng cách từ M đến ∆, kí hiệu là d(M , ∆), được tính bởi công thức sau:
d(M , ∆) = $\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$.
Chú ý: Nếu M ∈ ∆ thì d(M , ∆) = 0.
Ví dụ
a) Tính khoảng cách từ điểm O(0; 0) đến đường thẳng ∆: $\frac{x}{-4}+\frac{y}{2}=1$.
b) Tính khoảng cách giữa hai đường thẳng song song ∆1: x – y + 1 = 0 và ∆2: x – y – 1 = 0.
Giải
a) Ta có: $\frac{x}{-4}+\frac{y}{2}=1$ ⇔ x - 2y + 4 = 0.
Do đó, phương trình tổng quát của ∆ là x - 2y + 4 = 0.
Vậy d(O , ∆) = $\frac{|0-2.0+4|}{\sqrt{1^2+(-2)^2}}=\frac{4\sqrt{5}}{5}$ (đvđd).
b) Khoảng cách giữa hai đường thẳng song song là khoảng cách từ 1 điểm bất kì thuộc đường thẳng này đến đường thẳng kia (xem Hình).
Xét đường thẳng ∆1: x – y + 1 = 0, cho x = 0 ⇒ y = 1. Ta được điểm M(0 ; 1) ∈ ∆1. Ta có:
d(M , ∆2) = $\frac{|0-1-1|}{\sqrt{1^2+(-1)^2}}=\sqrt{2}$.
Vậy khoảng cách giữa hai đường thẳng song song ∆1 và ∆2 là $\sqrt{2}$ (đvđd).
Xem thêm các bài học khác :