Bài 5. Phương trình đường tròn
Chương VII. Phương pháp tọa độ trong mặt phẳng
1. Phương trình đường tròn
Phương trình đường tròn
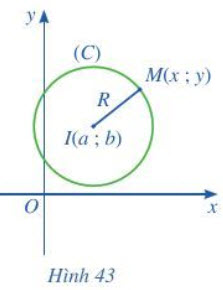
Phương trình đường tròn tâm I(a ; b) bán kính R (Hình 43) là
(x - a)2 + (y - b)2 = R2.
được gọi là phương trình chính tắc của đường tròn.
Nhận xét: (x - a)2 + (y - b)2 = R2 được đưa về dạng x2 + y2 - 2ax - 2by + c = 0 (với c = a2 + b2 - R2) được gọi là phương trình tổng quát của đường tròn.
Phương trình đường tròn đi qua ba điểm không thẳng hàng
Do có duy nhất một đường tròn đi qua ba điểm không thẳng hàng cho trước nên ta có thể lập được phương trình đường tròn đó khi biết tọa độ của ba điểm nói trên.
Ví dụ
1) Viết phương trình đường tròn tâm I(6 ; -4) đi qua điểm A(8 ; -7).
Giải
Đường tròn tâm I đi qua điểm A nên bán kính của đường tròn là
R = IA = $\sqrt{(8-6)^2+[(-7)-(-4)]^2}=\sqrt{13}$.
Vậy phương trình đường tròn (I) là (x – 6)2 + [y – (-4)]2 = $(\sqrt{13})^2$ hay (x – 6)2 + (y + 4)2 = 13.
2) Tìm k sao cho phương trình: x2 + y2 + 2kx + 4y + 6k – 1 = 0 (1) là phương trình đường tròn.
Giải
Ta có: (1) ⇔ (x2 + 2kx + k2) + (y2 + 4y + 4) = k2 + 4 - 6k + 1 ⇔ (x + k)2 + (y + 2)2 = k2 – 6k + 5
Do đó, phương trình (1) là phương trình đường tròn khi k2 – 6k + 5 > 0 (2).
Ta có: (2) ⇔ k ∈ (-∞ ; 1) ∪ (5 ; +∞).
Vậy để phương trình (1) là phương trình đường tròn thì k ∈ (-∞ ; 1) ∪ (5 ; +∞).
3) Lập phương trình đường tròn đi qua ba điểm A(1 ; 2), B(5 ; 2), C(1 ; -3).
Giải
Gọi tâm của đường tròn ngoại tiếp ∆ABC là điểm I(a ; b).
Ta có IA = IB = IC ⇔ IA2 = IB2 = IC2. Vì IA2 = IB2, IA2 = IC2 nên
$\left\{\begin{matrix}(1-a)^2+(2-b)^2=(5-a)^2+(2-b)^2\\(1-a)^2+(2-b)^2=(1-a)^2+(-3-b)^2\end{matrix}\right.$
⇔ $\left\{\begin{matrix}a^2+b^2-2a-4b+5=a^2+b^2-10a-4b+29\\a^2+b^2-2a-4b+5=a^2+b^2-2a+6b+10\end{matrix}\right.$
⇔ $\left\{\begin{matrix}8a=24\\-10b=5\end{matrix}\right.⇔\left\{\begin{matrix}a=3\\b=\frac{-1}{2}.\end{matrix}\right.$
Đường tròn tâm I(3 ; $\frac{-1}{2}$) có R2 = IA2 = (1 - 3)2 + (2 - $\frac{-1}{2}$)2 = $\frac{41}{4}$, phương trình là
(x - 3)2 + (y - $\frac{-1}{2}$)2 = $\frac{41}{4}$.
Vậy phương trình đường tròn ngoại tiếp ∆ABC là (x - 3)2 + (y + $\frac{1}{2}$)2 = $\frac{41}{4}$.
2. Phương trình tiếp tuyến của đường tròn
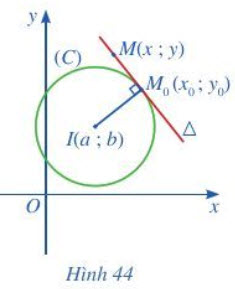
Cho đường tròn (C) tâm I(a ; b) và điểm M0(x0 ; y0) ∈ (C). Gọi ∆ là tiếp tuyến của (C) tại M0(x0 ; y0). Khi đó, ta có:
• Đường thẳng ∆ đi qua điểm M0(x0 ; y0) có vectơ pháp tuyến $\overrightarrow{IM}$ = (x0 - a ; y0 - b).
• Phương trình tiếp tuyến ∆ là
(x0 - a)(x - x0) + (y0 - b)(y - y0) = 0.
Ví dụ
Lập phương trình tiếp tuyến tại điểm M0(-1 ; -4) thuộc đường tròn (x – 3)2 + (y + 7)2 = 25.
Giải
Đường tròn (C) có tâm I(3 ; -7). Phương trình tiếp tuyến tại điểm M0(-1 ; -4) ∈ (C) là
(-1 – 3)[x – (-1)] + [(-4 – (-7)][y – (-4)] = 0
⇔ -4x – 4 + 3y + 12 = 0 ⇔ -4x + 3y + 8 = 0.
Xem thêm các bài học khác :