Bài 1. Tọa độ của vectơ
Chương VII. Phương pháp tọa độ trong mặt phẳng
1. Tọa độ của một điểm
Để xác định tọa độ của một điểm M tùy ý trong mặt phẳng tọa độ Oxy, ta làm như sau (Hình 3):
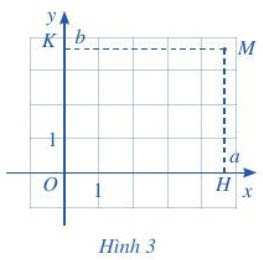
• Từ M kẻ đường vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.
• Từ M kẻ đường vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.
Cặp số (a ; b) là tọa độ của điểm M trong mặt phẳng tọa độ Oxy. Ta kí hiệu là M(a ; b).
2. Tọa độ của một vectơ
• Tọa độ của điểm M được gọi là tọa độ của vectơ $\overrightarrow{OM}$.
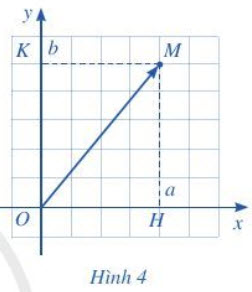
Nếu $\overrightarrow{OM}$ có tọa độ (a ; b) thì ta viết $\overrightarrow{OM}$ = (a ; b) hay $\overrightarrow{OM}$ (a ; b), trong đó a gọi là hoành độ của $\overrightarrow{OM}$, b gọi là tung độ của $\overrightarrow{OM}$ (Hình 4).
Chú ý: Trong mặt phẳng tọa độ Oxy (Hình 5), ta có:
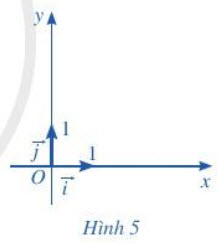
Vectơ ${\color{Blue}\overrightarrow{i}}$ có điểm gốc là O và có tọa độ (1 ; 0) gọi là vectơ đơn vị trên trục Ox.
Vectơ ${\color{Blue}\overrightarrow{u}}$ có điểm gốc là O và có tọa độ (0 ; 1) gọi là vectơ đơn vị trên trục Oy.
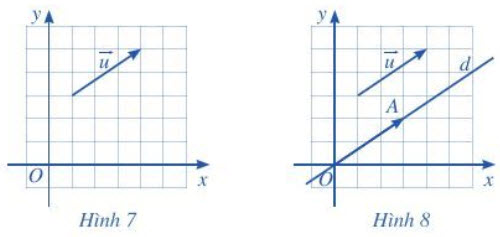
• Với mỗi vectơ $\overrightarrow{u}$ trong mặt phẳng tọa độ Oxy (Hình 7), tọa độ của vectơ $\overrightarrow{u}$ là tọa độ của điểm A, trong đó A là điểm sao cho $\overrightarrow{OA}=\overrightarrow{u}$ (Hình 8).
• Trong mặt phẳng tọa độ Oxy, nếu ${\color{Blue}\overrightarrow{u}=(a;b)}$ thì ${\color{Blue}\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}}$.
Ngược lại, nếu ${\color{Blue}\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}}$ thì ${\color{Blue}\overrightarrow{u}=(a;b)}$.
• Với $\overrightarrow{a}$ = (x1 ; y1) và $\overrightarrow{b}$ = (x2 ; y2), ta có:
$\overrightarrow{a}=\overrightarrow{b}⇔\left\{\begin{matrix}x_1=x_2\\y_1=y_2.\end{matrix}\right.$
Như vậy, mỗi vectơ hoàn toàn được xác định khi biết tọa độ của nó.
Ví dụ
1) Tìm tọa độ của các vectơ $\overrightarrow{c},\overrightarrow{d}$ trong Hình 11.
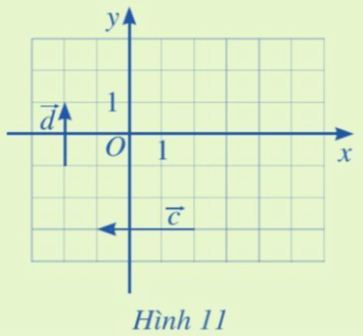
Giải
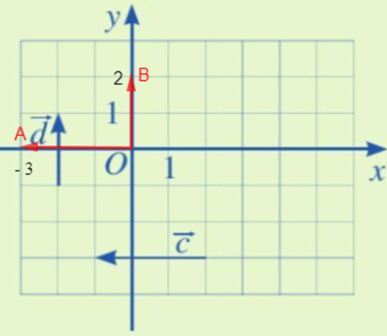
Quan sát Hình 11, ta xác định được:
• Điểm A(-3 ; 0) để $\overrightarrow{OA}=\overrightarrow{c}$ nên $\overrightarrow{c}$ = (-3 ; 0).
• Điểm B(0 ; 2) để $\overrightarrow{OB}=\overrightarrow{d}$ nên $\overrightarrow{d}$ = (0 ; 2).
2) Trong mặt phẳng tọa độ Oxy, cho điểm B(-1 ; 0) và vectơ $\overrightarrow{v}$ = (0 ; -7).
a) Biểu diễn vectơ $\overrightarrow{v}$ qua hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.
b) Biểu diễn vectơ $\overrightarrow{OB}$ qua hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.
Giải
a) $\overrightarrow{v}$ = (0 ; -7) ⇒ $\overrightarrow{v}=0.\overrightarrow{i}+(-7).\overrightarrow{j}=-7\overrightarrow{j}$.
b) B(-1 ; 0) nên $\overrightarrow{OB}$ = (-1 ; 0)
⇒ $\overrightarrow{OB}=(-1).\overrightarrow{i}+0.\overrightarrow{j}=-\overrightarrow{i}$.
3. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(xA ; yA) và B(xB ; yB). Ta có:
${\color{Blue}\overrightarrow{AB}=(x_B-x_A;y_B-y_A)}$.
Ví dụ
Trong mặt phẳng tọa độ Oxy, cho các điểm: A(1 ; 3), B(5 ; -1), C(2 ; -2), D(-2 ; 2). Chứng minh $\overrightarrow{AB}=\overrightarrow{DC}$.
Giải
Ta có: $\overrightarrow{AB}$ = (5−1 ; (-1)−3) = (4 ; -4); $\overrightarrow{DC}$ = (2−(-2) ; (-2)−2) = (4 ;−4).
Vậy $\overrightarrow{AB}=\overrightarrow{DC}$.
Xem thêm các bài học khác :