Bài 1. Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác
Chương IV. Hệ thức lượng trong tam giác. Vectơ
1. Giá trị lượng giác của một góc từ 0° đến 180°
♦ Với mỗi góc α (0° ≤ α ≤ 180°), ta xác định một điểm M(x0 ; y0) trên nửa đường tròn đơn vị (có bán kính là 1 đơn vị) sao cho $\widehat{xOM}$ = α (Hình 3). Khi đó:
• sin của góc α, kí hiệu là sin α, được xác định bởi: sin α = y0;
• côsin của góc α, kí hiệu là cos α, được xác định bởi: cos α = x0;
• tang của góc α, kí hiệu là tan α, được xác định bởi: tan α = ${\color{Blue}\frac{y_0}{x_0}}$ (x0 ≠ 0);
• côtang của góc α, kí hiệu là cot α, được xác định bởi: cot α = ${\color{Blue}\frac{x_0}{y_0}}$ (y0 ≠ 0).
Các số sin α, cos α, tan α, cot α được gọi là các giá trị lượng giác của góc α.
♦ Công thức biến đổi các giá trị lượng giác của một góc:
• tan α = $\frac{sinα}{cosα}$ (α ≠ 90°); cot α = $\frac{cosα}{sinα}$ (α ≠ 0°, α ≠ 180°).
• Với 0° ≤ α ≤ 90° thì:
sin (90° - α) = cos α;
cos (90° - α) = sin α;
tan (90° - α) = cot α (α ≠ 0°);
cot (90° - α) = tan α (α ≠ 90°).
• Với 0° ≤ α ≤ 90° thì:
sin (180° - α) = sin α;
cos (180° - α) = -cos α;
tan (180° - α) = -tan α (α ≠ 90°);
cot (180° - α) = -cot α (α ≠ 0°, α ≠ 180°).
Ví dụ
Cột cờ Lũng Cú (Hà Giang) nằm ở đỉnh Lũng Cú. Từ chân bệ cột cờ và đỉnh cột cờ bạn Nam đo được góc nâng (so với phương nằm ngang) tới một vị trí dưới chân núi lần lượt là 45° và 50° (xem Hình). Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi (trong bài toán ở phần mở đầu).
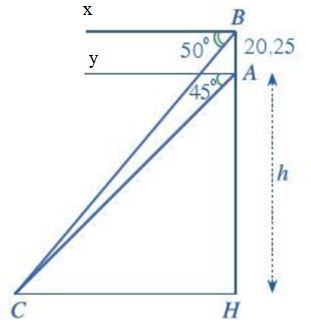
Giải
• xB // CD ⇒ $\widehat{BCH}=\widehat{xBC}$ = 50° (hai góc so le trong).
• $\widehat{yAC}$ = 45° ⇒ $\widehat{CAH}$ = 45°
do đó ∆CAH vuông cân tại H ⇒ HC = HA = h.
• Xét ∆CBH vuông tại H, ta có tan C = $\frac{HB}{HC}$
⇔ tan50° = $\frac{20,25+h}{h}$ ⇔ h ≈ 101,25 m.
Vậy chiều cao h của đỉnh Lũng Cú so với chân núi gần bằng 101,25 m.
2. Định lí côsin
Cho ∆ABC có BC = a, AC = b, AB = c. Khi đó:
a2 = b2 + c2 - 2bc.cosA ,
b2 = a2 + c2 - 2ac.cosB ,
c2 = a2 + b2 - 2ab.cosC .
cos A = $\frac{b^2+c^2-a^2}{2bc}$ ,
cos B = $\frac{a^2+c^2-b^2}{2ac}$ ,
cos C = $\frac{a^2+b^2-c^2}{2ab}$ .
Ví dụ
Cho tam giác ABC có AB = 5, AC = 6, BC = 7. Tính cos A.
Giải
Áp dụng định lí côsin trong tam giác ABC ta có:
BC2 = AB2 + AC2 - 2 AB . AC . cos A
⇔ 72 = 52 + 62 - 2.5.6.cos A
⇔ cos A = 0,2.
3. Định lí sin
Cho ∆ABC có BC = a, AC = b, AB = c và bán kính đường tròn ngoại tiếp là R. Khi đó:
$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$ = 2R.
a = 2R. sin A ,
b = 2R. sin B ,
c = 2R. sin C .
Ví dụ
Cho ∆ABC nội tiếp đường tròn (O) có bán kính R = 6 và có $\widehat{B}$ = 65°, $\widehat{C}$= 85°. Tính độ dài cạnh BC.
Giải
Ta có: $\widehat{A}=180°-(\widehat{B}+\widehat{C})$ = 180° - (65°+85°) = 30°.
Áp dụng định lí sin trong ∆ABC, ta có:
$\frac{BC}{sinA}$ = 2R
⇒ BC = 2R.sinA = 2.6.sin30° = 6.
Vậy BC = 6.
Xem thêm các bài học khác :