Bài 4. Hàm số lượng giác và đồ thị
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Hàm số lượng giác
2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
Cho hàm số y = f(x) với tập xác định D:
• Hàm số chẵn nếu với mọi x ∈ D ta có -x ∈ D và f(-x) = f(x).
Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
• Hàm số lẻ nếu với mọi x ∈ D ta có -x ∈ D và f(-x) = -f(x).
Đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Hàm số y = x2 là một ví dụ về hàm số chẵn (Hình 2a) và hàm số y = 2x là một ví dụ về hàm số lẻ (Hình 2b).
• Hàm số tuần hoàn nếu tồn tại một số T khác 0 sao cho với mọi x ∈ D ta có x ± T ∈ D và f(x + T) = f(x).
Số dương T nhỏ nhất thỏa mãn các điều kiện trên (nếu có) được gọi là chu kì của hàm số tuần hoàn y = f(x).
Đồ thị của hàm số tuần hoàn chu kì T được lặp lại trên từng đoạn giá trị của x có độ dài T.
Chú ý:
a) Các hàm số y = sin x và y = cos x là các hàm số tuần hoàn với chu kì 2π;
b) Các hàm số y = tan x và y = cot x là các hàm số tuần hoàn với chu kì π.
3. Đồ thị của các hàm số lượng giác
Hàm số y = sin x
Vẽ đồ thị của y = sin x trên đoạn [-π ; π] như phần đồ thị màu đỏ trong Hình 3. Sau đó lặp lại phần đồ thị này trên từng đoạn giá trị của x có độ dài 2π. Ta có đồ thị của hàm số y = sin x trên ℝ như sau:
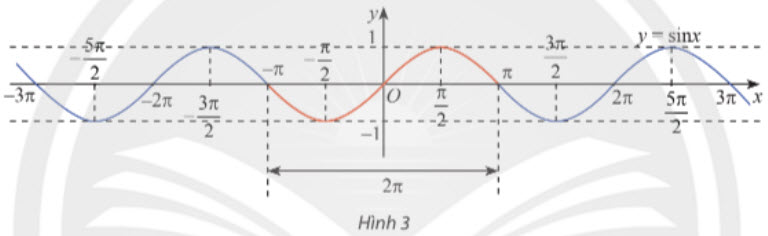
Từ đồ thị trên, ta thấy hàm số y = sin x có tập xác định là ℝ, tập giá trị là [-1 ; 1] và có các tính chất sau:
• Hàm số tuần hoàn với chu kì 2π.
• Hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.
• Hàm số đồng biến trên các khoảng $\left(\frac{-π}{2}+k2π;\frac{π}{2}+k2π\right)$ (k ∈ ℤ) và nghịch biến trên các khoảng $\left(\frac{π}{2}+k2π;\frac{3π}{2}+k2π\right)$ (k ∈ ℤ).
Hàm số y = cos x
Vẽ đồ thị của y = cos x trên đoạn [-π ; π] như phần đồ thị màu đỏ trong Hình 4. Sau đó lặp lại phần đồ thị này trên từng đoạn giá trị của x có độ dài 2π. Ta có đồ thị của hàm số y = cos x trên ℝ như sau:
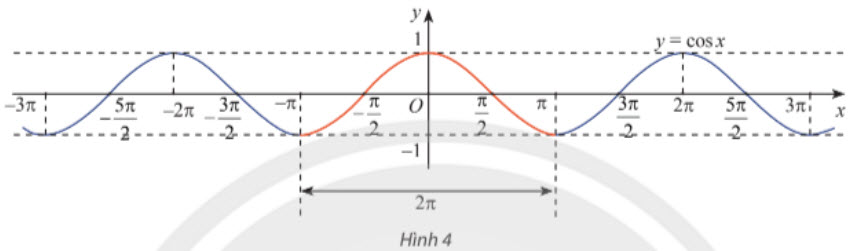
Từ đồ thị trên, ta thấy hàm số y = cos x có tập xác định là ℝ, tập giá trị là [-1 ; 1] và có các tính chất sau:
• Hàm số tuần hoàn với chu kì 2π.
• Hàm số chẵn, có đồ thị đối xứng qua trục Oy.
• Hàm số đồng biến trên các khoảng (-π + k2π ; k2π) (k ∈ ℤ) và nghịch biến trên các khoảng (k2π ; π + k2π) (k ∈ ℤ) (k ∈ ℤ).
Hàm số y = tan x
Vẽ đồ thị của y = tan x trên khoảng $\left(\frac{-π}{2};\frac{π}{2}\right)$ như phần đồ thị màu đỏ trong Hình 7. Sau đó lặp lại phần đồ thị này trên từng đoạn giá trị của x có độ dài π. Ta có đồ thị của hàm số y = tan x trên ℝ \ $\left\{\frac{π}{2}+2π|k∈ℤ\right\}$ như sau:
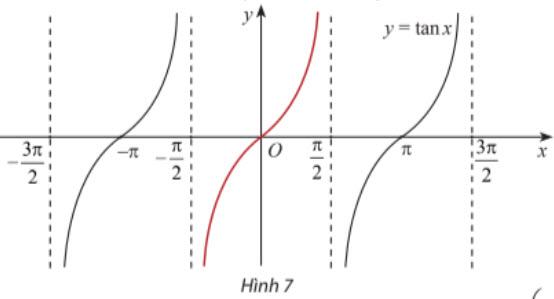
Từ đồ thị trên, ta thấy hàm số y = tan x có tập xác định là ℝ \ $\left\{\frac{π}{2}+2π|k∈ℤ\right\}$, tập giá trị là ℝ và có các tính chất sau:
• Hàm số tuần hoàn với chu kì π.
• Hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.
• Hàm số đồng biến trên các khoảng $\left(\frac{-π}{2}+kπ;\frac{π}{2}+kπ\right)$ (k ∈ ℤ).
Hàm số y = cot x
Vẽ đồ thị của y = cot x trên khoảng (0 ; π) như phần đồ thị màu đỏ trong Hình 8. Sau đó lặp lại phần đồ thị này trên từng đoạn giá trị của x có độ dài π. Ta có đồ thị của hàm số y = cot x trên ℝ \ {kπ | k ∈ ℤ} như sau:
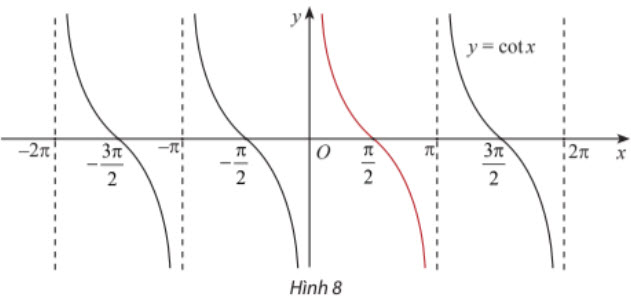
Từ đồ thị trên, ta thấy hàm số y = cot x có tập xác định là ℝ \ {kπ | k ∈ ℤ}, tập giá trị là ℝ và có các tính chất sau:
• Hàm số tuần hoàn với chu kì π.
• Hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.
• Hàm số nghịch biến trên các khoảng (kπ ; π + kπ) (k ∈ ℤ).
Ví dụ
Cho hàm số y = cos x với x ∈ $\left[\frac{-π}{2};π\right]$
a) Vẽ đồ thị hàm số đã cho.
b) Tại các điểm nào thì giá trị của hàm số lớn nhất ?
c) Tìm các giá trị của x thuộc $\left[-\frac{π}{4};\frac{5π}{4}\right]$ sao cho sin$\left(x-\frac{π}{4}\right)$ < 0.
Giải
a) Trên mặt phẳng Oxy, lấy các điểm (x ; cos x) như sau: $\left(\frac{-π}{2};0\right),(0;1),\left(\frac{π}{2};0\right),(π;-1)$, ta có đồ thị hàm số như hình dưới.
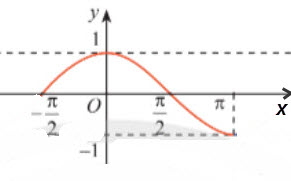
b) Từ đồ thị trên, giá trị của hàm số lớn nhất bằng 1 tại điểm (0 ; 1).
c) Ta có sin$\left(x-\frac{π}{4}\right)$ = cos$\left[\frac{π}{2}-\left(x-\frac{π}{4}\right)\right]$ = cos$\left(\frac{3π}{4}-x\right)$.
Đặt t = $\frac{3π}{4}-x$. Vì $\frac{-π}{4}≤x≤\frac{5π}{4}$ nên $\frac{-π}{2}≤t≤π$. Từ đồ thị trên, ta có:
sin$\left(x-\frac{π}{4}\right)$ < 0 ⇔ cos t < 0 ⇔ $\frac{π}{2}
suy ra $\frac{π}{2}<\frac{3π}{4}-x<π$ ⇔ $\frac{-π}{4}
Xem thêm các bài học khác :