Bài 2. Giá trị lượng giác của một góc lượng giác
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
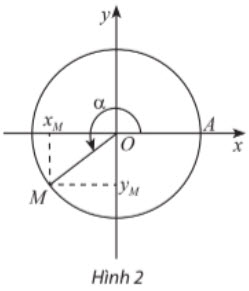
1. Giá trị lượng giác của góc lượng giác
Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo α (Hình 2). Khi đó:
• Tung độ yM của M gọi là sin của α, kí hiệu sin α.
• Hoành độ xM của M gọi là côsin của α, kí hiệu cos α.
• Nếu xM ≠ 0 thì tỉ số ${\color{Blue}\frac{y_M}{x_M}=\frac{sinα}{cosα}}$ gọi là tang của α, kí hiệu tan α.
• Nếu yM ≠ 0 thì tỉ số ${\color{Blue}\frac{x_M}{y_M}=\frac{cosα}{sinα}}$ gọi là côtang của α, kí hiệu cot α.
Các giá trị sin α, cos α, tan α và cot α được gọi là các giá trị lượng giác của góc lượng giác α.
Chú ý:
a) Ta gọi trục hoành là trục côsin, còn trục tung là trục sin.
Trục As có gốc ở điểm A(1; 0) và song song với trục sin (Hình 3a) gọi là trục tang. Nếu đường thẳng OM cắt trục tang thì tung độ của giao điểm đó chính là tan α.
Trục Bs có gốc ở điểm A(0; 1) và song song với trục côsin (Hình 3b) gọi là trục côtang. Nếu đường thẳng OM cắt trục côtang thì hoành độ của giao điểm đó chính là cot α.
b) sin α và cos α xác định với mọi α ∈ ℝ;
tan α chỉ xác định với các góc α ≠ $\frac{π}{2}$ + kπ (k ∈ ℤ);
cot α chỉ xác định với các góc α ≠ kπ (k ∈ ℤ).
c) Với mọi góc lượng giác α và số nguyên k, ta có:
sin (α + k2π) = sin α; cos (α + k2π) = cos α;
tan (α + kπ) = tan α; cot (α + kπ) = cot α.
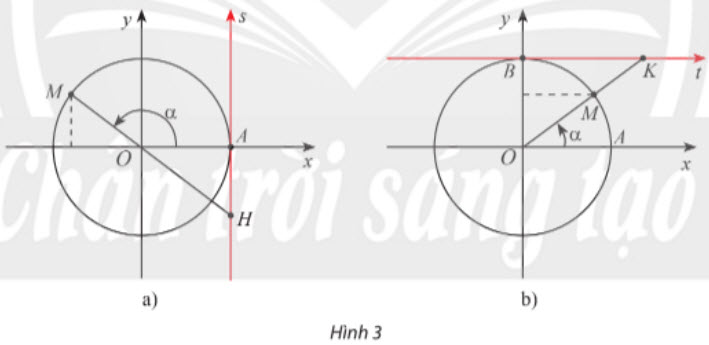
2. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
• sin2 α +cos2 α = 1;
• tan α . cot α = 1 với α ≠ k$\frac{π}{2}$, k ∈ ℤ;
• 1 + tan2 α = $\frac{1}{cos^2α}$ với α ≠ $\frac{π}{2}$ + kπ, k ∈ ℤ;
• 1 + cot2 α = $\frac{1}{sin^2α}$ với α ≠ kπ, k ∈ ℤ;
Ví dụ
Cho tan α = $\frac{2}{3}$ với π < α < $\frac{3π}{2}$. Tính cos α và sin α.
Giải
Ta có: $\frac{1}{cos^2α}$ = 1 + tan2 α = 1 + $\left(\frac{2}{3}\right)^2=\frac{13}{9}$
⇒ cos α = $\frac{3}{\sqrt{13}}$ (loại) hoặc cos α = $\frac{-3}{\sqrt{13}}$ (nhận)
(Vì π < α < $\frac{3π}{2}$ nên điểm biểu diễn của góc α trên đường tròn lượng giác thuộc góc phần tư thứ III, do đó cos α < 0).
Ta có sin α = tan α . cos α = $\frac{2}{3}.\frac{-3}{\sqrt{13}}=\frac{-2}{\sqrt{13}}$.
3. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
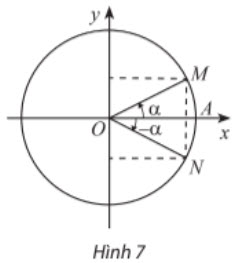
Hai góc đối nhau: α và -α
Các điểm biểu diễn của hai góc đối nhau α và -α đối xứng nhau qua trục Ox (Hình 7), nên ta có:
sin (-α) = -sin α
cos (-α) = cos α
tan (-α) = -tan α
cot (-α) = -cot α
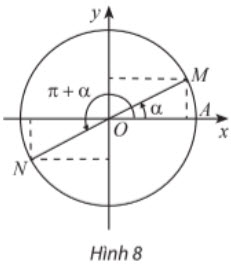
Hai góc hơn kém nhau π: α và α + π
Các điểm biểu diễn của hai góc α và α + π đối xứng nhau qua gốc tọa độ O (Hình 8), nên ta có:
sin (α + π) = -sin α
cos (α + π) = -cos α
tan (α + π) = tan α
cot (α + π) = cot α
Hai góc bù nhau: α và π - α
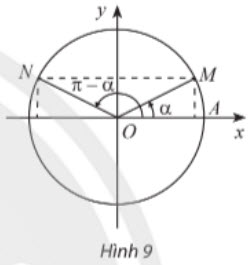
Các điểm biểu diễn của hai góc α và π - α đối xứng nhau qua trục Oy (Hình 9), nên ta có:
sin (π - α) = sin α
cos (π - α) = -cos α
tan (π - α) = -tan α
cot (π - α) = -cot α
Hai góc phụ nhau: α và $\frac{π}{2}$ - α
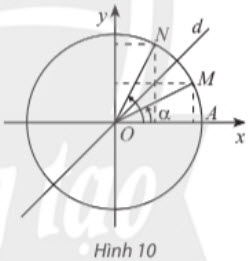
Các điểm biểu diễn của hai góc α và$\frac{π}{2}$ - α đối xứng nhau qua đường phân giác d của góc xOy (Hình 10), nên ta có:
sin$\left(\frac{π}{2}-α\right)$ = cos α; cos$\left(\frac{π}{2}-α\right)$ = sin α
tan$\left(\frac{π}{2}-α\right)$ = cot α; cot$\left(\frac{π}{2}-α\right)$ = tan α
Ví dụ
a) Biểu diễn cos 638° qua giá trị lượng giác của góc có số đo từ 0° đến 45°.
b) Biểu diễn cot$\frac{19π}{5}$ qua giá trị lượng giác của góc có số đo từ 0 đến $\frac{π}{4}$.
Giải
a) cos 638° = cos(2.360° + (-82°)) = cos(-82°) = cos82° = sin(90° – 82°) = sin 8°.
b) cot$\frac{19π}{5}$ = cot$\left(4π-\frac{π}{5}\right)$ = cot$\left(-\frac{π}{5}\right)$ = -cot$\frac{π}{5}$.
Xem thêm các bài học khác :