Bài 1. Góc lượng giác
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Góc lượng giác
Khái niệm góc lượng giác
Khi xét chuyển động quay của một tia Om quanh gốc O của nó tính từ vị trí ban đầu Oa theo một chiều cố định, người ta quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm. Một vòng quay theo chiều dương tương ứng với góc quay 360°, một vòng quay theo chiều âm tương ứng với góc quay -360°.
Cho hai tia Oa, Ob.
• Nếu một tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob, kí hiệu (Oa, Ob).
• Khi tia Om quay một góc α, ta nói số đo của góc lượng giác (Oa, Ob) bằng α, kí hiệu sđ(Oa, Ob) = α.
Chú ý: Với hai tia Oa và Ob cho trước, có vô số góc lượng giác tia đầu Oa và tia cuối Ob. Ta dùng chung kí hiệu (Oa, Ob) cho tất cả các góc lượng giác này.
Nhận xét: Số đo của các góc lượng giác (Oa, Ob) sai khác nhau một bội nguyên của 360° nên có công thức tổng quát là:
sđ(Oa, Ob) = α° + k 360° (k ∈ ℤ)
thường viết là (Oa, Ob) = α° + k 360° , với α° là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob. Chẳng hạn, trong Hình 5, (Oa, Ob) = 90° + k 360° (k ∈ ℤ).
Hệ thức Chasles (Sa-lơ)
Với ba tia Oa, Ob và Oc bất kì, ta có:
(Oa, Ob) + (Ob, Oc) = (Oa, Oc) + k 360° (k ∈ ℤ).
Ví dụ
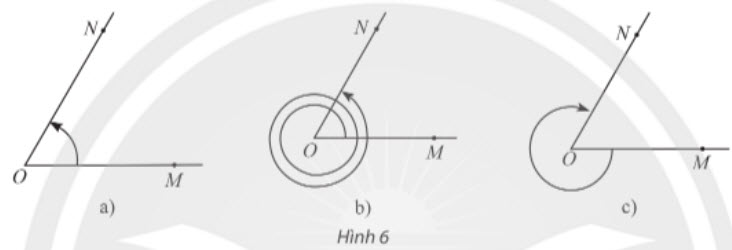
1) Cho $\widehat{MON}$ = 60°. Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM, ON).
Giải
Số đo góc lượng giác (OM, ON) trong Hình 6a là 60°.
Số đo góc lượng giác (OM, ON) trong Hình 6b là 60° + 2.360° = 780°.
Số đo góc lượng giác (OM, ON) trong Hình 6c là –(360° – 60°) = –300°.
Công thức tổng quát của số đo góc lượng giác (OM, ON) là 60° + k 360° (k ∈ ℤ).
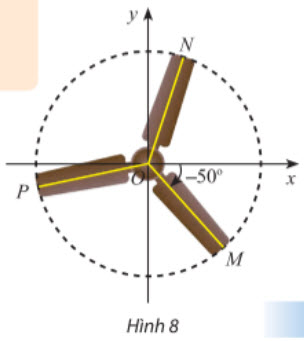
2) Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox, ON) và (Ox, OP).
Giải
Chiếc quạt có ba cạnh được phân bố đều nhau nên $\widehat{MON}=\widehat{NOP}=\widehat{POM}$ = 120°. Ta có (Ox, OM) = -50°.
• Áp dụng hệ thức Chasles cho ba tia Ox, OM và ON, ta có:
(Ox, ON) = (Ox, OM) + (OM, ON) + k360° = -50° + 120° + k 360° = 70° + k 360°.
• Áp dụng hệ thức Chasles cho ba tia Ox, ON và OP, ta có:
(Ox, OP) = (Ox, ON) + (ON, OP) + k360° = 70° + 120° + k 360° = 190° + k 360°.
2. Đơn vị radian
Trên đường tròn bán kính R tùy ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (đọc là 1 ra-đi-an, viết tắt là 1 rad) (Hình 9).
Ta có:
• 180° = π rad.
• 1° = $\frac{π}{180}$ rad ≈ 0,0175 rad.
• 1 rad = $\left(\frac{180}{π}\right)°$ ≈ 57,3° (hay 57°17'45").
Chú ý:
a) Khi ghi số đo của một góc theo đơn vị radian, người ta thường bỏ đi chữ rad sau số đo. Ví dụ: $\frac{π}{2}$ rad được viết là $\frac{π}{2}$, 2 rad được viết là 2.
b) Với đơn vị radian, công thức số đo tổng quát của góc lượng giác (Oa, Ob) là α + k2π (k ∈ ℤ), trong đó α là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
Lưu ý không được viết α + k360° hay a° + k2π (vì không cùng đơn vị đo).
Ví dụ
Đổi các số đo góc sau đây từ radian sang độ hoặc ngược lại: -60°; $\frac{2π}{5}$ rad; 3 rad.
Giải
• -60° = -60.$\frac{π}{180}$ rad = $\frac{-π}{3}$ rad.
• $\frac{2π}{5}$ rad = $\left(\frac{2π}{5}.\frac{180}{π}\right)°$ = 72°.
• 3 rad = $\left(3.\frac{180}{π}\right)°=\left(\frac{540}{π}\right)°$ ≈ 172°.
3. Đường tròn lượng giác
Trong mặt phẳng tọa độ Oxy, cho đường tròn (O; 1), chọn điểm A(1; 0) làm gốc, chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là chiều cùng chiều kim đồng hồ. Đường tròn cùng với gốc và chiều như trên được gọi là đường tròn lượng giác (Hình 11).
Cho số đo góc α bất kì. Trên đường tròn lượng giác, ta xác định được duy nhất một điểm M sao cho sđ(OA, OM) = α (Hình 12). Khi đó điểm M được gọi là điểm biểu diễn của góc có số đo α trên đường tròn lượng giác.
Ví dụ
Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:
a) -1485°; b) $\frac{19π}{4}$.
Giải
a) Ta có: -1485° = -45° + (-4).360°. Điểm biểu diễn góc có số đo -1485° là điểm B trên đường tròn lượng giác sao cho (OA, OB) = -45°.
b) Ta có:$\frac{19π}{4}=\frac{3π}{4}$ + 2.2π. Điểm biểu diễn góc có số đo $\frac{19π}{4}$ rad là điểm C trên đường tròn lượng giác sao cho (OA, OC) = $\frac{3π}{4}$ rad (hay 135°).
Xem thêm các bài học khác :