Bài 4. Bất phương trình bậc hai một ẩn
Chương III. Hàm số và đồ thị
1. Bất phương trình bậc hai một ẩn
Ví dụ
• Các bất phương trình: x2 - x - 1 > 0; -2x2 + 3x ≤ 0; x2 - 2 ≥ 0 là bất phương trình bậc hai ẩn x.
• Các bất phương trình: x2 - y > 0; 2x3 - x + 1 < 0 không phải là bất phương trình bậc hai ẩn x.
2. Giải bất phương trình bậc hai một ẩn
Giải bất phương trình bậc hai ẩn x là đi tìm tập nghiệm của bất phương trình đó.
Ta xét dạng f(x) > 0 với f(x) = ax2 + bx + c (a ≠ 0), các dạng f(x) ≥ 0, f(x) < 0, f(x) ≤ 0 được giải tương tự.
Xét dấu của tam thức bậc hai
Tập nghiệm của f(x) > 0 là tập hợp các giá trị của x sao cho f(x) mang dấu +.
Sử dụng đồ thị
• Tập nghiệm của f(x) > 0 là tập hợp các giá trị của x ứng với phần parabol y = f(x) nằm phía trên trục hoành.
• Tập nghiệm của f(x) < 0 là tập hợp các giá trị của x ứng với phần parabol y = f(x) nằm phía dưới trục hoành.
Ứng dụng của bất phương trình bậc hai một ẩn
Tính toán lợi nhuận trong klnh doanh; tính toán điểm rơi trong pháo binh; ...
Ví dụ
1) Giải các bất phương trình bậc hai sau:
a) 3x2 - 2x + 4 ≤ 0 (1); b) x2 - 4x + 3 > 0 (2).
Giải
a) f(x) = 3x2 - 2x + 4 có ∆ = (-2)2 - 4. 3. 4 = -44 < 0 và a = 3 > 0 nên f(x) > 0 với ∀x ∈ ℝ.
Vậy bất phương trình (1) vô nghiệm.
b) f(x) = x2 - 4x + 3 có hai nghiệm x1 = 1, x2 = 3. Ta có bảng xét dấu của f(x) như sau:
x
-∞
1
3
+∞
f(x)
+
0
-
0
+
Vậy tập nghiệm của bất phương trình (2) là (-∞ ; 1) ∪ (3 ; +∞).
Cách sử dụng đồ thị:
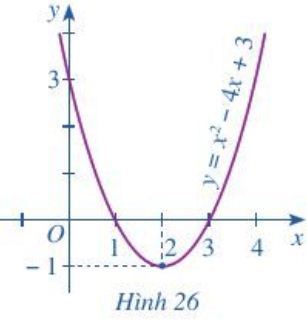
Quan sát parabol (P): y = x2 - 4x + 3 ở Hình 26, ta thấy:
• Phần (P) nằm ở phía trên trục hoành: có y > 0 ứng với x < 1 hoặc x > 3.
• Phần (P) nằm ở phía dưới trục hoành: có y < 0 ứng với 1 < x < 3.
• (P) cắt trục hoành tại hai điểm (1 ; 0) , (3 ; 0) hay y = 0 ứng với x = 1 hoặc x = 3.
Vậy tập nghiệm của bất phương trình (2) là (-∞ ; 1) ∪ (3 ; +∞).
2) Tổng chi phí T (đơn vị: nghìn đồng) để sản xuất Q sản phẩm được cho bởi biểu thức T = Q2 + 30Q + 3300; giá bán của 1 sản phẩm là 170 nghìn đồng. Số sản phẩm được sản xuất trong khoảng nào để đảm bảo có lãi (giả thiết các sản phẩm được bán hết)?
Giải
Theo đề bài, ta có Q ∈ ℕ*, doanh thu bán Q sản phẩm là 170.Q (nghìn đồng).
Để đảm bảo có lãi thì 170Q ≥ T ⇔170Q ≥ Q2 + 30Q + 3300 ⇔ Q2 - 140Q + 3300 ≤ 0.
Ta xét dấu A = Q2 - 140Q + 3300. Biểu thức A có hai nghiệm là Q1 = 30, Q2 = 110 và a = 1 > 0.
x
-∞
30
110
+∞
A
+
0
-
0
+
Do đó, A ≤ 0 ⇔ 30 ≤ Q ≤ 110.
Vậy để đảm bảo có lãi thì phải sản xuất từ 30 đến 110 sản phẩm.
Xem thêm các bài học khác :