Bài 3. Hai đường thẳng song song
Chương 4. Góc và đường thẳng song song
1. Hai góc so le trong. Hai góc đồng vị
2. Dấu hiệu nhận biết hai đường thẳng song song
• Hai đường thẳng a và b không có điểm nào chung thì được gọi là hai đường thẳng song song, kí hiệu a // b hoặc b // a.
• Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.
Trong Hình 4a, hai đường thẳng m và n song song vì chúng tạo với đường thẳng d hai góc đồng vị bằng nhau.
Trong Hình 4b, hai đường thẳng c và d song song vì chúng tạo với đường thẳng h hai góc so le trong bằng nhau.
Chú ý: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
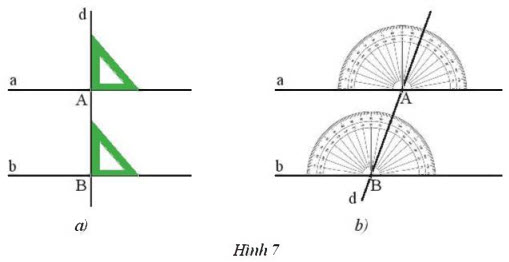
Cách vẽ hai đường thẳng a và b song song
• Vẽ a, b cùng vuông góc với đường thẳng d (Hình 7a).
• Vẽ a, b cùng cùng tạo với đường thẳng d hai góc so le trong hoặc đồng vị bằng nhau (Hình 7b).
Ví dụ
Cho hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B (Hình 6). Hãy chứng tỏ a // b.
Giải
a ⊥ c tại A nên $\widehat{A_1}$ = 90°.
b ⊥ c tại B nên $\widehat{B_1}$ = 90°.
Ta có, $\widehat{A_1}=\widehat{B_1}$ = 90° (hai góc đồng vị bằng nhau) nên a // b.
3. Tiên đề Euclid về đường thẳng song song
Tiên đề Euclid: Qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Cho điểm M nằm ngoài đường thẳng a. Đường thẳng b đi qua M và song song với đường thẳng a là duy nhất (Hình 9).
Chú ý: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
a // c và b // c suy ra a // b (Hình 10).
4. Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau và hai góc đồng vị bằng nhau.
Cho a // b và c cắt a, b lần lượt tại A, B. Ta có:
• $\widehat{A_1}=\widehat{B_3};\widehat{A_4}=\widehat{B_2}$ (hai góc so le trong bằng nhau).
• $\widehat{A_1}=\widehat{B_1};\widehat{A_2}=\widehat{B_2};\widehat{A_3}=\widehat{B_3};\widehat{A_4}=\widehat{B_4}$ (hai góc đồng vị bằng nhau).
Chú ý: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại (Hình 14).
a // b và c ⊥ a suy ra c ⊥ b.
Ví dụ
Cho biết m // n và a // b. Tính số đo x, y, z, t của các góc trong Hình 12.
.jpg)
Giải
Hỉnh 12a, m // n nên:
• $\widehat{D_1}=\widehat{ACD}$ = 135° (hai góc đồng vị). Do đó x = 135°.
• $\widehat{A_1}=\widehat{ABD}$ = 80° (hai góc so le trong). Do đó y = 80°.
Hỉnh 12b, a // b nên:
• $\widehat{aMN}=\widehat{MNF}$ = 60° (hai góc so le trong).
Mặt khác $\widehat{NME}+\widehat{aMN}$ = 180° (hai góc kề bù)
suy ra $\widehat{NME}$ = 180° - $\widehat{aMN}$ = 180° - 60° = 120°. Do đó z = 120°.
• $\widehat{E_1}=\widehat{EFN}$ (hai góc so le trong)
Mặt khác EF⊥ NF tại F nên $\widehat{EFN}$ = 90°, suy ra $\widehat{E_1}$ = 90°. Do đó t = 90°.
Xem thêm các bài học khác :