Bài 2. Tia phân giác

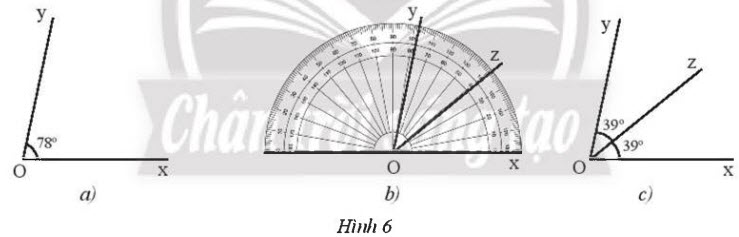
Vẽ tia phân giác của $\widehat{xOy}$ có số đo 78° (Hình 6a).

- Ta có $\widehat{xOz}=\widehat{yOz}$ và $\widehat{xOz}+\widehat{yOz}$ = 78° nên suy ra $\widehat{xOz}$ = 78° : 2 = 39°.

- Dùng thước đo góc vẽ tia Oz đi qua một điểm trong của $\widehat{xOy}$ sao cho $\widehat{xOz}$ = 39° (Hình 6b).

- Ta được tia Oz là tia phân giác của $\widehat{xOy}$ (Hình 6c).

Chú ý: Ta gọi đường thẳng chứa tia phân giác của một góc là đường phân giác của góc đó.

Trong Hình 7, đường thẳng zt là đường phân giác của góc xOy.