Bài 4. Tích vô hướng của hai vectơ
Chương 5. Vectơ
1. Góc giữa hai vectơ
Ví dụ
Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc: $\left(\overrightarrow{AB},\overrightarrow{AC}\right),\left(\overrightarrow{AB},\overrightarrow{BC}\right),\left(\overrightarrow{AH},\overrightarrow{BC}\right),\left(\overrightarrow{BH},\overrightarrow{BC}\right),\left(\overrightarrow{HB},\overrightarrow{BC}\right)$.
Giải
∆ABC là tam giác đều có H là trung điểm của cạnh BC nên các góc của ∆ABC đều bằng 60°, AH ⊥ BC.
• $\left(\overrightarrow{AB},\overrightarrow{AC}\right)=\widehat{BAC}$ = 60°.
• Vẽ đường thẳng qua A song song với BC, trên đó lấy M sao cho $\overrightarrow{AM}=\overrightarrow{BC}$, ta có $\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\widehat{BAM}$.
AM // BC ⇒ $\widehat{BAM}=180°-\widehat{ABC}$ = 180° - 60° = 120°. Vậy $\left(\overrightarrow{AB},\overrightarrow{BC}\right)$ = 120°.
• $\left(\overrightarrow{AH},\overrightarrow{BC}\right)$ = 90° (vì AH ⊥ BC).
• $\left(\overrightarrow{BH},\overrightarrow{BC}\right)$ = 0° (vì $\overrightarrow{BH}$ và $\overrightarrow{BC}$ cùng hướng).
• $\left(\overrightarrow{HB},\overrightarrow{BC}\right)$ = 180° (vì $\overrightarrow{HB}$ và $\overrightarrow{BC}$ ngược hướng).
2. Tích vô hướng của hai vectơ
Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác $\overrightarrow{0}$.
Tích vô hướng của $\overrightarrow{a}$ và $\overrightarrow{b}$ là một số, kí hiệu là ${\color{Blue}\overrightarrow{a}.\overrightarrow{b}}$, được xác định bởi công thức:
$\overrightarrow{a}.\overrightarrow{b}=|\overrightarrow{a}|.|\overrightarrow{b}|.cos\left(\overrightarrow{a}.\overrightarrow{b}\right)$.
Chú ý:
• Khi một trong hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng $\overrightarrow{0}$, ta quy ước ${\color{Blue}\overrightarrow{a}.\overrightarrow{b}=0}$.
• Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, ta có ${\color{Blue}\overrightarrow{a}⊥\overrightarrow{b}⇔\overrightarrow{a}.\overrightarrow{b}=0}$.
• Khi $\overrightarrow{a}=\overrightarrow{b}$ thì tích vô hướng $\overrightarrow{a}.\overrightarrow{b}$ được kí hiệu là $\overrightarrow{a}^2$ và được gọi là bình phương vô hướng của vectơ $\overrightarrow{a}$.
Ta có ${\color{Blue}\overrightarrow{a}^2=|\overrightarrow{a}|.|\overrightarrow{a}|.cos0°=|\overrightarrow{a}|^2}$. Vậy bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.
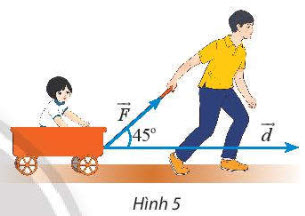
• Trong Vật lí, tích vô hướng của $\overrightarrow{F}$ và $\overrightarrow{d}$ biểu diễn công A sinh bởi lực $\overrightarrow{F}$ khi thực hiện độ dịch chuyển $\overrightarrow{d}$ (xem Hình 5).
Ta có công thức: ${\color{Blue}A=\overrightarrow{F}.\overrightarrow{d}}$.
Ví dụ
Cho tam giác ABC vuông cân tại A, cạnh huyền bằng $\sqrt{2}$. Tính các tích vô hướng: $\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{AC}.\overrightarrow{BC},\overrightarrow{BA}.\overrightarrow{BC}$.
Giải
∆ABC vuông cân tại A, có BC = $\sqrt{2}$ nên ta tính được $\widehat{B}=\widehat{C}$ = 45°, AB = AC = 1.
• $\widehat{A}$ = 90° ⇒ $\overrightarrow{AB}⊥\overrightarrow{AC}$. Vậy $\overrightarrow{AB}.\overrightarrow{AC}$ = 0.
• $\overrightarrow{AC}.\overrightarrow{BC}$ = AC.BC. cos$(\overrightarrow{AC}.\overrightarrow{BC})$ = 1.$\sqrt{2}$. cos45° = 1.
• $\overrightarrow{BA}.\overrightarrow{BC}$ = BA.BC. cosB = 1.$\sqrt{2}$. cos45° = 1.
3. Tính chất của tích vô hướng
Với ba vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ bất kì và mọi số k, ta có:
$\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}$;
$\overrightarrow{a}.(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}$;
$(k\overrightarrow{a}).\overrightarrow{b}=k(\overrightarrow{a}.\overrightarrow{b})=\overrightarrow{a}.(k\overrightarrow{b})$.
Nhận xét:
• $(\overrightarrow{a}+\overrightarrow{b})^2=\overrightarrow{a}^2+2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2$;
• $(\overrightarrow{a}-\overrightarrow{b})^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2$;
• $(\overrightarrow{a}+\overrightarrow{b}).(\overrightarrow{a}-\overrightarrow{b})=\overrightarrow{a}^2-\overrightarrow{b}^2$.
Ví dụ
Cho hai vectơ $\overrightarrow{i},\overrightarrow{j}$ vuông góc, cùng có độ dài bằng 1. Cho $\overrightarrow{a}=2\overrightarrow{i}+2\overrightarrow{j},\overrightarrow{b}=3\overrightarrow{i}-3\overrightarrow{j}$. Tính tích vô hướng $\overrightarrow{a}.\overrightarrow{b}$ và tính góc $\left(\overrightarrow{a},\overrightarrow{b}\right)$.
Giải
• $\overrightarrow{a}.\overrightarrow{b}=\left(2\overrightarrow{i}+2\overrightarrow{j}\right).\left(3\overrightarrow{i}-3\overrightarrow{j}\right)$
= $2\left(\overrightarrow{i}+\overrightarrow{j}\right).3\left(\overrightarrow{i}-\overrightarrow{j}\right)$
= $6\left(\overrightarrow{i}^2-\overrightarrow{j}^2\right)=6\left(|\overrightarrow{i}|^2-|\overrightarrow{j}|^2\right)$ = 6.(12 - 12) = 0.
• $\overrightarrow{a}.\overrightarrow{b}$ = 0 ⇒ $\overrightarrow{a}⊥\overrightarrow{b}$. Vậy $\left(\overrightarrow{a},\overrightarrow{b}\right)$ = 90°.
Xem thêm các bài học khác :