Bài 3. Tích của một số với một vectơ
Chương 5. Vectơ
1. Tích của một số với một vectơ và các tính chất
♦ Cho số k khác 0 và vectơ $\overrightarrow{a}$ khác $\overrightarrow{0}$. Tích của số k với vectơ $\overrightarrow{a}$ là một vectơ, kí hiệu là ${\color{Blue}k\overrightarrow{a}}$.
Vectơ ${\color{Blue}k\overrightarrow{a}}$ cùng hướng với $\overrightarrow{a}$ nếu k > 0, ngược hướng với $\overrightarrow{a}$ nếu k < 0 và có độ dài bằng ${\color{Blue}|k|.|\overrightarrow{a}|}$.
Ta quy ước ${\color{Blue}0\overrightarrow{a}=\overrightarrow{0}}$ và ${\color{Blue}k\overrightarrow{0}=\overrightarrow{0}}$.
♦ Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bất kì, với mọi số thực h và k, ta có:
$k\left(\overrightarrow{a}+\overrightarrow{b}\right)=k\overrightarrow{a}+k\overrightarrow{b}$;
$(h+k)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a}$;
$h(k\overrightarrow{a})=(hk)\overrightarrow{a}$;
$1.\overrightarrow{a}=\overrightarrow{a}$;
$(-1).\overrightarrow{a}=-\overrightarrow{a}$.
Ví dụ
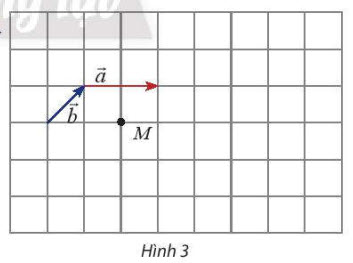
Cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$ và một điểm M như Hình 3.
a) Hãy vẽ các vectơ $\overrightarrow{MN}=3\overrightarrow{a},\overrightarrow{MP}=-3\overrightarrow{b}$.
b) Cho biết mỗi ô vuông có cạnh bằng 1. Tính: $|3\overrightarrow{b}|,|-3\overrightarrow{b}|,|2\overrightarrow{a}+2\overrightarrow{b}|$.
Giải
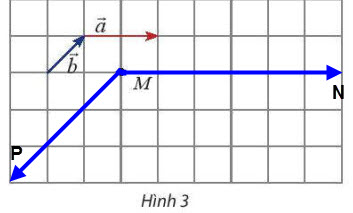
a) • Ta vẽ $\overrightarrow{MN}=3\overrightarrow{a}$ như sau:
Qua M ta vẽ đường thẳng song song với giá của $\overrightarrow{a}$, trên đường thẳng đó lấy điểm N sao cho $\overrightarrow{MN}$ cùng hướng với $\overrightarrow{a}$ và MN = 3.$|\overrightarrow{a}|$.
• Ta vẽ $\overrightarrow{MP}=-3\overrightarrow{b}$ như sau:
Qua M ta vẽ đường thẳng song song với giá của $\overrightarrow{b}$, trên đường thẳng đó lấy điểm P sao cho $\overrightarrow{MP}$ ngược hướng với $\overrightarrow{b}$ và MP = 3.$|\overrightarrow{b}|$.
b) Mỗi ô vuông có cạnh bằng 1 nên $|\overrightarrow{a}|=2,|\overrightarrow{b}|=\sqrt{2}$.
• $|3\overrightarrow{b}|=3.|\overrightarrow{b}|=3\sqrt{2}$,
• $|-3\overrightarrow{b}|=|-3|.|\overrightarrow{b}|=3\sqrt{2}$,
• $2\overrightarrow{a}+2\overrightarrow{b}=2(\overrightarrow{a}+\overrightarrow{b})=2\overrightarrow{BC}$ (xem Hình với $\overrightarrow{a}=\overrightarrow{AC},\overrightarrow{b}=\overrightarrow{BA}$ ).
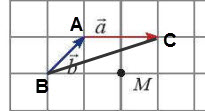
Xét ∆ABC, ta có: $\widehat{A}$ = 45° + 90° = 135°, theo định lí côsin thì
BC2 = AB2 + AC2 – 2.AB.AC.cosA = $(\sqrt{2})^2$ + 22 – 2.$\sqrt{2}$.2.cos135° = 10
⇒ BC = $\sqrt{10}$.
Vậy $|2\overrightarrow{a}+2\overrightarrow{b}|=|2\overrightarrow{BC}|$ = 2.BC = $2\sqrt{10}$.
2. Điều kiện để hai vectơ cùng phương
• Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương, $\overrightarrow{b}$ khác $\overrightarrow{0}$ khi và chi khi có số k sao cho ${\color{Blue}\overrightarrow{a}=k\overrightarrow{b}}$.
• Ba điểm phân biệt A, B, C thẳng hàng khi và chi khi có số k khác 0 để ${\color{Blue}\overrightarrow{AB}=k\overrightarrow{AC}}$.
• Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ không cùng phương. Với mỗi vectơ $\overrightarrow{c}$ luôn tồn tại duy nhất cặp số thực (m; n) sao cho ${\color{Blue}\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}}$.
Ví dụ
Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$. Chứng minh ba điểm I, G, J thẳng hàng.
Giải
I là trung điểm của AB nên $\overrightarrow{GA}+\overrightarrow{GB}=2\overrightarrow{GI}$.
J là trung điểm của CD nên $\overrightarrow{GC}+\overrightarrow{GD}=2\overrightarrow{GJ}$.
Ta có: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$
⇔ $2\overrightarrow{GI}+2\overrightarrow{GJ}=\overrightarrow{0}$
⇔ $2(\overrightarrow{GI}+\overrightarrow{GJ})=\overrightarrow{0}$
⇔ $\overrightarrow{GI}+\overrightarrow{GJ}=\overrightarrow{0}$.
Do đó G là trung điểm của IJ. Vậy ba điểm I, G, J thẳng hàng.
Xem thêm các bài học khác :