Bài 1. Khái niệm vectơ
Chương 5. Vectơ
Chúng ta cần vectơ để biểu diễn các đại lượng có hướng.
1. Định nghĩa vectơ
Ví dụ
Cho tam giác đều ABC có cạnh bằng 2. Gọi H là trung điểm của đoạn thẳng BC.
Tìm điểm đầu, điểm cuối, giá và độ dài của các vectơ $\overrightarrow{CH},\overrightarrow{CB},\overrightarrow{HA}$.
Giải
• Vectơ $\overrightarrow{CH}$ có điểm đầu là C, điểm cuối là H và có giá là đường thẳng CH.
Độ dài của $\overrightarrow{CH}$ là $|\overrightarrow{CH}|$ = CH = $\frac{BC}{2}=\frac{2}{2}$ = 1 (do H là trung điểm của BC).
• Vectơ $\overrightarrow{CB}$ có điểm đầu là C, điểm cuối là B và có giá là đường thẳng BC.
Độ dài của $\overrightarrow{CB}$ là $|\overrightarrow{CB}|$ = CB = 2.
• Vectơ $\overrightarrow{HA}$ có điểm đầu là H, điểm cuối là A và có giá là đường thẳng AH.
Độ dài của $\overrightarrow{HA}$ là $|\overrightarrow{HA}|$ = HA = AC.sinC = 2.sin60° = $\sqrt{3}$.
2. Hai vectơ cùng phương, cùng hướng
Ví dụ
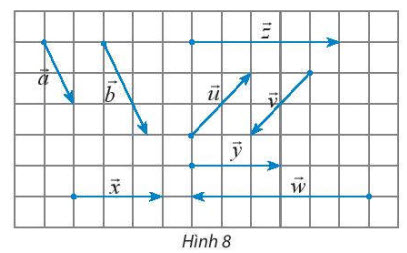
Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ $\overrightarrow{x}$;
b) Cùng hướng với vectơ $\overrightarrow{a}$;
c) Ngược hướng với vectơ $\overrightarrow{u}$.
Giải
a) Các vectơ $\overrightarrow{w},\overrightarrow{y},\overrightarrow{z}$ cùng phương với vectơ $\overrightarrow{x}$ (vì chúng có giá trùng nhau hoặc song song với giá của vectơ $\overrightarrow{x}$).
b) Vectơ $\overrightarrow{b}$ cùng hướng với vectơ $\overrightarrow{a}$ (vì chúng có giá song song với nhau và có cùng hướng trên Hình 8).
c) Vectơ $\overrightarrow{v}$ ngược hướng với vectơ $\overrightarrow{u}$ (vì chúng có giá song song với nhau và có hướng ngược nhau trên Hình 8).
3. Vectơ bằng nhau, vectơ đối nhau
• Hai vectơ $\overrightarrow{a},\overrightarrow{b}$ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu ${\color{Blue}\overrightarrow{a}=\overrightarrow{b}}$ (xem Hình 11a).
• Hai vectơ $\overrightarrow{a},\overrightarrow{b}$ được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu ${\color{Blue}\overrightarrow{a}=-\overrightarrow{b}}$. Khi đó, vectơ $\overrightarrow{b}$ được gọi là vectơ đối của vectơ $\overrightarrow{a}$ (xem Hình 11b).
Chú ý:
• Cho vectơ $\overrightarrow{a}$ và điểm O, ta luôn tìm được một điểm A duy nhất sao cho $\overrightarrow{OA}=\overrightarrow{a}$. Khi đó độ dài của vectơ $\overrightarrow{a}$ là độ dài đoạn thẳng OA, kí hiệu là $|\overrightarrow{a}|$ (xem Hình 12).
• Cho đoạn thẳng MN, ta luôn có $\overrightarrow{NM}=-\overrightarrow{MN}$.
Ví dụ
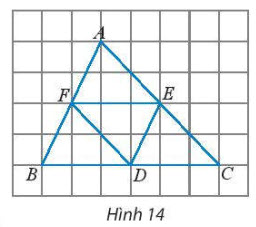
Cho D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC (Hình 14).
a) Tìm các vectơ bằng vectơ $\overrightarrow{EF}$.
b) Tìm các vectơ đối của vectơ $\overrightarrow{EC}$.
Giải
a) EF là đường trung bình của ∆ABC nên EF // BC và EF = $\frac{BC}{2}$.
D là trung điểm của BC nên BD = DC = $\frac{BC}{2}$.
Do đó EF = BD = DC và EF // BD, EF // DC.
Vậy các vectơ bằng vectơ $\overrightarrow{EF}$ là $\overrightarrow{DB},\overrightarrow{CD}$.
b) FD là đường trung bình của ∆ABC nên FD // AC và FD = $\frac{AC}{2}$.
E là trung điểm của AC nên EC = AE = $\frac{AC}{2}$.
Do đó: EC = AE = FD và FD // EC.
Vậy các vectơ đối của vectơ $\overrightarrow{EC}$ là $\overrightarrow{CE},\overrightarrow{EA},\overrightarrow{DF}$.
4. Vectơ-không
Ví dụ
Cho đoạn thẳng EF có độ dài bằng 2 và nhận M là trung điểm. Tìm độ dài của các vectơ $\overrightarrow{EF},\overrightarrow{EE},\overrightarrow{EM},\overrightarrow{MM},\overrightarrow{FF}$.
Giải
• Các vectơ $\overrightarrow{EE}=\overrightarrow{MM}=\overrightarrow{FF}=\overrightarrow{0}$ nên $|\overrightarrow{EE}|=|\overrightarrow{MM}|=|\overrightarrow{FF}|$ = 0.
• $|\overrightarrow{EF}|$ = EF = 2.
• $|\overrightarrow{EM}|$ = EM = EF : 2 = 2 : 2 = 1 (vì M là trung điểm của EF).
Xem thêm các bài học khác :