Bài 4. Ba đường conic trong mặt phẳng tọa độ
Chương 9. Phương pháp tọa độ trong mặt phẳng
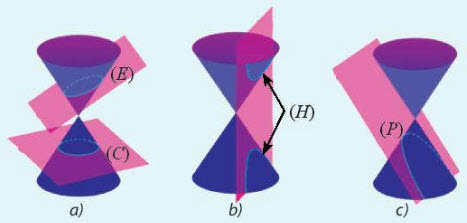
Nếu cắt mặt nón tròn xoay bởi mặt phẳng vuông góc với trục và không đi qua đỉnh của mặt nón thì ta thu được một đường tròn (C).
Nếu thay đổi vị trí của mặt phẳng, ta sẽ có thêm các loại "đường" khác như hình trên, các đường đó gọi là các đường conic.
1. Elip
Nhận biết elip
Cho hai điểm cố định F1, F2 và một độ dài không đổi 2a lớn hơn F1F2. Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho F1M + F2M = 2a.
Các điểm F1 và F2 gọi là các tiêu điểm của elip. Độ dài F1F2 = 2c gọi là tiêu cự của elip (a > c).
Phương trình chính tắc của elip
Chọn hệ trục tọa độ Oxy sao cho F1(-c; 0) và F2(c; 0) (xem Hình 3), ${\color{Blue}b=\sqrt{a^2-c^2}}$, ta có phương trình chính tắc của elip (E) là:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Chú ý:
• (E) cắt Ox tại hai điểm A1(-a; 0), A2(a; 0) và cắt Oy tại hai điểm B1(0; -b), B2(0; b). Các điểm A1, A2, B1, B2 gọi là các đỉnh của elip.
• Đoạn thẳng A1A2 gọi là trục lớn, đoạn thẳng B1B2 gọi là trục nhỏ của elip.
• Giao điểm O của hai trục gọi là tâm đối xứng của elip.
• Nếu M(x; y) ∈ (E) thì |x| ≤ a, |y| ≤ b.
Ví dụ
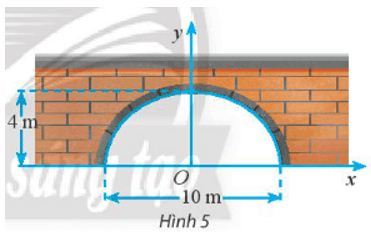
Một đường hầm có mặt cắt hình nửa elip cao 4m, rộng 10m (Hình 5). Viết phương trình chính tắc của elip đó.
Giải
Theo Hình 5, ta có: 2a = 10 ⇔ a = 5 và b = 4.
Vậy phương trình chính tắc của elip đó là:
$\frac{x^2}{5^2}+\frac{y^2}{4^2}=1⇔\frac{x^2}{25}+\frac{y^2}{16}=1$.
2. Hypebol
Nhận biết hypebol
Cho hai điểm cố định F1, F2 và một độ dài không đổi 2a nhỏ hơn F1F2. Hypebol (H) là tập hợp các điểm M trong mặt phẳng sao cho |F1M - F2M| = 2a.
Các điểm F1 và F2 gọi là các tiêu điểm của hypebol. Độ dài F1F2 = 2c gọi là tiêu cự của hypebol (c > a).
Phương trình chính tắc của elip
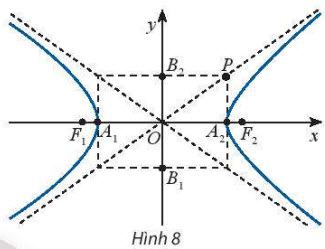
Chọn hệ trục tọa độ Oxy sao cho F1(-c; 0) và F2(c; 0) (xem Hình 8), ${\color{Blue}b=\sqrt{c^2-a^2}}$, ta có phương trình chính tắc của hypebol (H) là:
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
Chú ý:
• (H) cắt Ox tại hai điểm A1(-a; 0), A2(a; 0). Các điểm A1, A2 gọi là các đỉnh của hypebol.
• Đoạn thẳng A1A2 gọi là trục thực, đoạn thẳng B1B2 (với B1(0; -b), B2(0; b) ) gọi là trục ảo của hypebol.
• Giao điểm O của hai trục gọi là tâm đối xứng của hypebol.
• Nếu M(x; y) ∈ (H) thì x ≤ -a hoặc x ≥ a.
Ví dụ
Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục ảo bằng 6.
Giải
Tiêu cự của hypebol là 2c = 10 ⇔ c = 5 và độ dài trục ảo là 2b = 6 ⇔ b = 3.
Ta có: a = $\sqrt{c^2-b^2}=\sqrt{5^2-3^2}$ = 4.
Phương trình chính tắc của hypebol là:
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
⇔ $\frac{x^2}{4^2}-\frac{y^2}{3^2}=1⇔\frac{x^2}{16}-\frac{y^2}{9}=1$.
3. Parabol
Nhận biết parabol
Cho một điểm F cố định và một đường thẳng ∆ cố định không đi qua F. Parabol (P) là tập hợp các điểm M cách đều F và ∆.
F gọi là các tiêu điểm và ∆ gọi là đường chuẩn của parabol (P).
Phương trình chính tắc của parabol
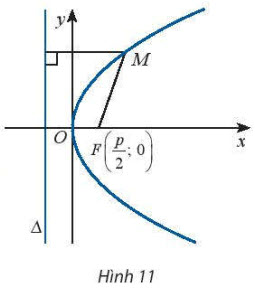
Chọn hệ trục tọa độ Oxy sao cho $F\left(\frac{p}{2};0\right)$ và ∆: $x+\frac{p}{2}=0$ (xem Hình 11), ta có phương trình chính tắc của parabol (P) là:
y2 = 2px.
Chú ý:
• O gọi là đỉnh của parabol.
• Ox gọi là trục đối xứng của parabol.
• p gọi là tham số tiêu của parabol.
• Nếu M(x; y) ∈ (P) thì x ≥ 0 và M'(x; -y) ∈ (P).
Ví dụ
Viết phương trình chính tắc của parabol (P) có đường chuẩn ∆: x + 1 = 0.
Giải
Ta có đường chuẩn ∆: x + 1 = 0 nên $\frac{p}{2}$ = 1 ⇔ p = 2.
Vậy (P) có phương trình: y2 = 2. 2. x ⇔ y2 = 4x.
Xem thêm các bài học khác :