Bài 3. Đường tròn trong mặt phẳng tọa độ
Chương 9. Phương pháp tọa độ trong mặt phẳng
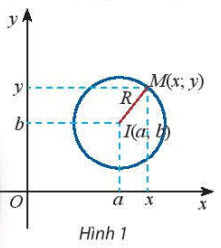
1. Phương trình đường tròn
Trong mặt phẳng Oxy, đường tròn tâm I(a; b) bán kính R (xem Hình 1), có phương trình là:
(x - a)2 + (y - b)2 = R2.
Ngược lại, phương trình x2 + y2 - 2ax - 2by + c = 0 là phương trình đường tròn (C) khi và chỉ khi a2 + b2 - c > 0.
Khi đó đường tròn (C) có tâm I(a; b) vá bán kính R = ${\color{Blue}\sqrt{a^2+b^2-c}}$.
Ví dụ
1) Viết phương trình đường tròn (C) có tâm I(2; -2), bán kính R = 8.
Giải
Đường tròn (C) tâm I(2; -2), bán kính R = 8 có phương trình:
(x - 2)2 + [y - (-2)]2 = 82 ⇔ (x - 2)2 + (y + 2)2 = 64.
2) Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.
a) x2 + y2 – 2x – 4y – 20 = 0;
b) 2x2 + 2y2 + 6x + 8y – 2 = 0.
Giải
a) Phương trình đã cho có dạng x2 + y2 – 2ax – 2by + c = 0 với a = 1, b = 2 và c = -20.
Ta có: a2 + b2 – c = 12 + 22 – (-20) = 25 > 0.
Vậy đây là phương trình đường tròn có tâm I(1; 2) và bán kính R = $\sqrt{25}$ = 5.
b) 2x2 + 2y2 + 6x + 8y – 2 = 0
⇔ x2 + y2 + 3x + 4y – 1 = 0
Phương trình đã cho có dạng x2 + y2 – 2ax – 2by + c = 0 với a = $\frac{-3}{2}$, b = -2 và c = -1.
Ta có: a2 + b2 – c = $\left(\frac{-3}{2}\right)^2$ + (-2)2 − (-1) = $\frac{29}{4}$ > 0.
Vậy đây là phương trình đường tròn có tâm $I\left(\frac{-3}{2};-2\right)$ và bán kính R = $\sqrt{\frac{29}{4}}=\frac{\sqrt{29}}{2}$.
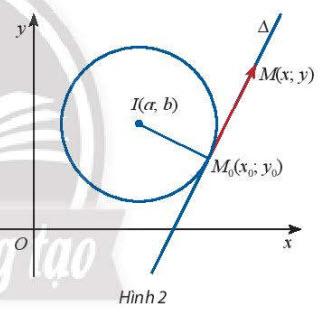
2. Phương trình tiếp tuyến của đường tròn
Phương trình tiếp tuyến của đường tròn tâm I(a; b) tại điểm M0(x0; y0) nằm trên đường tròn là:
(a - x0)(x - x0) + (b - y0)(y - y0) = 0.
Ví dụ
Viết phương trình tiếp tuyến của đường tròn (C): x2 + y2 – 2x – 4y – 20 = 0 tại điểm A(4; 6).
Giải
x2 + y2 – 2x – 4y – 20 = 0
⇔ (x – 1)2 + (y – 2)2 = 52
Do đó phương trình đường tròn (C) có tâm I(1; 2) và bán kính R = 5.
IA = $\sqrt{(4-1)^2+(6-2)^2}$ = 5 ⇒ A ∈ (C)
Phương trình tiếp tuyến của (C) tại điểm A(4; 6) ∈ (C) là:
(1 – 4)(x – 4) + (2 – 6)(y – 6) = 0
⇔ 3x + 4y – 36 = 0.
Xem thêm các bài học khác :