Bài 1. Tọa độ của vectơ
Chương 9. Phương pháp tọa độ trong mặt phẳng
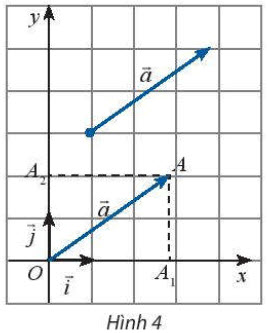
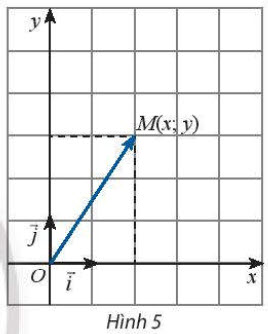
1. Tọa độ của vectơ đối với một hệ trục tọa độ
Trục tọa độ
Trục tọa độ (gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm O (gọi là điểm gốc) và một vectơ ${\color{Blue}\overrightarrow{e}}$ có độ dài bằng 1 gọi là vectơ đơn vị của trục.
Ta kí hiệu trục đó là ${\color{Blue}(O;\overrightarrow{e})}$ (xem Hình 2).
Hệ trục tọa độ
Hệ trục tọa độ ${\color{Blue}(O;\overrightarrow{i},\overrightarrow{j})}$ gồm hai trục ${\color{Blue}(O;\overrightarrow{i})}$ và ${\color{Blue}(O;\overrightarrow{j})}$ vuông góc với nhau. Điểm gốc O chung của hai trục gọi là gốc tọa độ.
Trục ${\color{Blue}(O;\overrightarrow{i})}$ gọi là trục hoành và kí hiệu là Ox, trục ${\color{Blue}(O;\overrightarrow{j})}$ gọi là trục tung và kí hiệu là Oy. Các vectơ ${\color{Blue}\overrightarrow{i}}$ và ${\color{Blue}\overrightarrow{j}}$ là các vectơ đơn vị trên Ox và Oy. Hệ trục tọa độ ${\color{Blue}(O;\overrightarrow{i},\overrightarrow{j})}$ còn được kí hiệu là Oxy (xem Hình 3).
Chú ý: Mặt phẳng mà trên đó đã cho một hệ trục tọa độ Oxy được gọi là mặt phẳng tọa độ Oxy (hay gọi tắt là mặt phẳng Oxy).
Tọa độ của vectơ
Trong mặt phẳng Oxy, cặp số (x; y) trong biểu diễn ${\color{Blue}\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}}$ được gọi là tọa độ của vectơ ${\color{Blue}\overrightarrow{a}}$, kí hiệu ${\color{Blue}\overrightarrow{a}=(x;y)}$, x gọi là hoành độ, y gọi là tung độ của vectơ ${\color{Blue}\overrightarrow{a}}$ (xem Hình 4).
Chú ý:
• $\overrightarrow{a}=(x;y)⇔\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}$.
• Nếu cho $\overrightarrow{a}=(x;y)$ và $\overrightarrow{b}=(x';y')$ thì $\overrightarrow{a}=\overrightarrow{b}⇔\left\{\begin{matrix}x=x'\\y=y'.\end{matrix}\right.$
Tọa độ của một điểm
Trong mặt phẳng tọa độ, cho một điểm M tùy ý. Tọa độ của vectơ $\overrightarrow{OM}$ được gọi là tọa độ của điểm M (xem Hình 5).
Nhận xét:
• Nếu $\overrightarrow{OM}$ = (x; y) thì cặp số (x; y) là tọa độ của điểm M, kí hiệu M(x; y), x gọi là hoành độ, y gọi là tung độ của điểm M.
• $M(x;y)⇔\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}$.
Chú ý: Hoành độ của điểm M còn được kí hiệu là xM, tung độ của điểm M còn được kí hiệu là yM. Khi đó ta viết M(xM; yM).
Ví dụ
Trong mặt phẳng Oxy, cho ba điểm D(-1; 4), E(0; -3), F(5; 0).
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy.
b) Tìm tọa độ của các vectơ $\overrightarrow{OD},\overrightarrow{OE},\overrightarrow{OF}$.
c) Vẽ và tìm tọa độ hai vectơ đơn vị $\overrightarrow{i}$ và $\overrightarrow{j}$ lần lượt trên hai trục tọa độ Ox và Oy.
Giải
a) Các điểm D, E, F được vẽ trên mặt phẳng Oxy như sau:
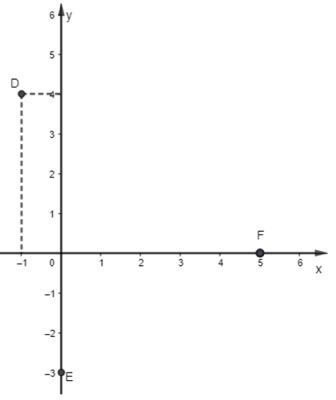
b) D(-1; 4) nên tọa độ của vectơ $\overrightarrow{OD}$ = (-1; 4).
E(0; -3) nên tọa độ của vectơ $\overrightarrow{OE}$ = (0; -3).
F(5; 0) nên tọa độ của vectơ $\overrightarrow{OF}$ = (5; 0).
c) Hai vectơ đơn vị $\overrightarrow{i}$ và $\overrightarrow{j}$ được vẽ lần lượt trên hai trục tọa độ Ox và Oy như sau:
Tọa độ của vectơ $\overrightarrow{i}$ = (1; 0) và tọa độ của vectơ $\overrightarrow{j}$ = (0; 1).
2. Biểu thức tọa độ của các phép toán vectơ
Cho hai vectơ $\overrightarrow{a}$ = (a1; a2), $\overrightarrow{b}$ = (b1; b2) và số thực k. Khí đó:
• $\overrightarrow{a}+\overrightarrow{b}$ = (a1+ b1; a2 + b2);
• $\overrightarrow{a}-\overrightarrow{b}$ = (a1- b1; a2 - b2);
• $k\overrightarrow{a}$ = (ka1; ka2);
• $\overrightarrow{a}.\overrightarrow{b}$ = a1.b1 + a2.b2.
Ví dụ
Cho hai vectơ $\overrightarrow{m}$ = (-6; 1) và $\overrightarrow{n}$ = (0; 2).
a) Tìm tọa độ của các vectơ $\overrightarrow{m}+\overrightarrow{n},\overrightarrow{m}-\overrightarrow{n},10\overrightarrow{m},-4\overrightarrow{n}$.
b) Tính các tích vô hướng $\overrightarrow{m}.\overrightarrow{n},(10\overrightarrow{m}).(-4\overrightarrow{n})$.
Giải
a) $\overrightarrow{m}+\overrightarrow{n}$ = (-6 + 0; 1 + 2) = (-6; 3).
$\overrightarrow{m}-\overrightarrow{n}$ = (-6 – 0; 1 – 2) = (-6; -1);
$10\overrightarrow{m}$ = (10.(-6); 10.1) = (-60; 10);
$-4\overrightarrow{n}$ = ( (-4).0; (-4).2) = (0; -8).
b) $\overrightarrow{m}.\overrightarrow{n}$ = (-6).0 + 1.2 = 2;
$(10\overrightarrow{m}).(-4\overrightarrow{n})$ = -60.0 + 10.(-8) = -80.
3. Áp dụng của tọa độ vectơ
Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng
Cho hai điểm A(xA; yA), B(xB; yB). Ta có:
$\overrightarrow{AB}=(x_B-x_A;y_B-y_A)$.
Tọa độ trung điểm của đoạn thẳng và trọng tâm của tam giác
• Cho hai điểm A(xA; yA) và B(xB; yB). Tọa độ trung điểm M(xM; yM) của đoạn thẳng AB là:
$x_M=\frac{x_A+x_B}{2},y_M=\frac{y_A+y_B}{2}$.
• Cho tam giác ABC có A(xA; yA), B(xB; yB), C(xC; yC). Tọa độ trọng tâm G(xG; yG) của tam giác ABC là:
$x_G=\frac{x_A+x_B+x_C}{3},y_G=\frac{y_A+y_B+y_C}{3}$.
Ví dụ
1) Cho E(9; 9), F(8; -7), G(0; -6). Tìm tọa độ của các vectơ $\overrightarrow{FE},\overrightarrow{FG},\overrightarrow{EG}$.
Giải
• $\overrightarrow{FE}=(x_E-x_F;y_E-y_F)$ = (9 – 8; 9 – (-7) ) = (1; 16);
• $\overrightarrow{FG}=(x_G-x_F;y_G-y_F)$ = (0 – 8; -6 – (-7) ) = (-8; 1);
• $\overrightarrow{EG}=(x_G-x_E;y_G-y_E)$ = (0 – 9; -6 – 9) = (-9; -15).
2) Cho tam giác QRS có tọa độ các đỉnh là Q(7; -2), R(-4; 9) và S(5; 8).
a) Tìm tọa độ trung điểm M của cạnh QS.
b) Tìm tọa độ trọng tâm G của tam giác QRS.
Giải
a) Trung điểm M(xM; yM) của cạnh QS với Q(7; -2), S(5; 8) là:
$x_M=\frac{x_Q+x_S}{2}=\frac{7+5}{2}=6,y_M=\frac{y_Q+y_S}{2}=\frac{-2+8}{2}=3$.
Vậy M(6; 3).
b) Trọng tâm G(xG; yG) của ∆QRS với Q(7; -2), R(-4; 9), S(5; 8) là:
$x_G=\frac{x_Q+x_R+x_S}{3}=\frac{7+(-4)+5}{3}=\frac{8}{3},y_G=\frac{y_Q+y_R+y_S}{3}=\frac{-2+9+8}{3}=5$.
Vậy $G\left(\frac{8}{3};5\right)$.
4. Ứng dụng biểu thức tọa độ của các phép toán vectơ
Cho hai vectơ $\overrightarrow{a}$ = (a1; a2), $\overrightarrow{b}$ = (b1; b2) và hai điểm A(xA; yA), B(xB; yB). Ta có:
• $\overrightarrow{a}⊥\overrightarrow{b}$ ⇔ a1.b1 + a2.b2 = 0;
• $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương ⇔ a1.b2 - a2.b1 = 0;
• $\left|\overrightarrow{a}\right|=\sqrt{a_1^2+a_2^2}$;
• AB = $\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$;
• $cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{|\overrightarrow{a}|.|\overrightarrow{b}|}=\frac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}.\sqrt{b_1^2+b_2^2}}$ ($\overrightarrow{a},\overrightarrow{b}$ khác $\overrightarrow{0}$).
Ví dụ
Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ các đỉnh là D(2; 2), E(6; 2) và F(2; 6).
a) Tìm tọa độ điểm H là chân đường cao của tam giác DEF kẻ từ D.
b) Giải tam giác DEF.
Giải
$\overrightarrow{a}⊥\overrightarrow{b}$ ⇔ a1.b1 + a2.b2 = 0;
a) Xét H(x; y). Ta có: $\overrightarrow{DH}$ = (x-2; y-2), $\overrightarrow{EH}$ = (x-6; y-2), $\overrightarrow{EF}$ = (2-6; 6-2) = (-4; 4).
H là chân đường cao của tam giác DEF kẻ từ D, nên ta có:
• $\overrightarrow{DH}⊥\overrightarrow{EF}$ ⇔ (x-2).(-4) + (y-2).4 = 0 ⇔ -x + y = 0; (1)
• $\overrightarrow{EH},\overrightarrow{EF}$ cùng phương ⇔ (x-6).4 - (y-2).(-4) = 0 ⇔ x + y = 8. (2)
Giải hệ (1) và (2), ta được x = 4 và y = 4. Vậy H(4; 4).
b) Ta có: $\overrightarrow{DE}$ = (4; 0), $\overrightarrow{EF}$ = (-4; 4), $\overrightarrow{DF}$ = (2-6; 6-2) = (0; 4), suy ra:
DE = $\sqrt{4^2+0^2}$ = 4, EF = $\sqrt{(-4)^2+4^2}=4\sqrt{2}$, DF = $\sqrt{0^2+4^2}$ = 4.
∆DEF có DE = DF (= 4) và EF2 = DE2 + DF2 (do $(4\sqrt{2})^2$ = 42 + 42 (= 32) )
⇒ ∆DEF vuông cân tại D. Do đó: $\widehat{D}=90°,\widehat{E}=45°,\widehat{F}=45°$.
Xem thêm các bài học khác :