Bài 3. Đường tiệm cận của đồ thị hàm số
Chương I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
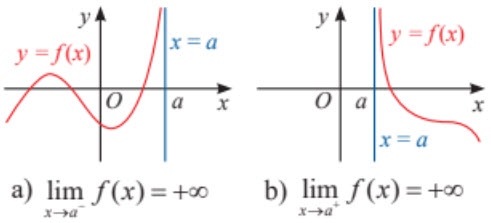
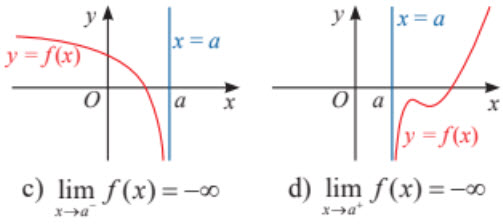
1. Đường tiệm cận đứng
Đường thẳng x = a gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu có ít nhất một trong các điều kiện sau:
$\underset{x\rightarrow a^-}{lim}\;f(x)=+\infty,\underset{x\rightarrow a^+}{lim}\;f(x)=+\infty,\underset{x\rightarrow a^-}{lim}\;f(x)=-\infty,\underset{x\rightarrow a^+}{lim}\;f(x)=-\infty$.
Ví dụ
Tìm tiệm cận đứng của đồ thị hàm số $y=f(x)=\frac{2x+3}{-x+5}$.
Giải
Tập xác định D = ℝ \ {5}.
Ta có $\underset{x\rightarrow5^-}{lim}\;f(x)=+\infty$.
Vậy đường thẳng x = 5 là một tiệm cận đứng của đồ thị hàm số.
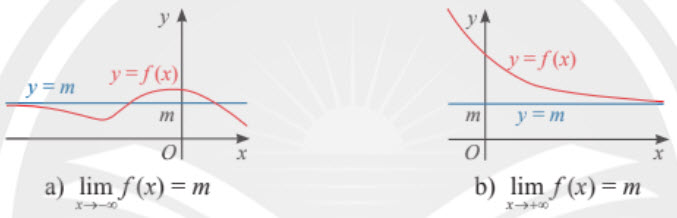
2. Đường tiệm cận ngang
Đường thẳng y = m gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu
$\underset{x\rightarrow-\infty}{lim}\;f(x)=m$ hoặc $\underset{x\rightarrow+\infty}{lim}\;f(x)=m$.
Ví dụ
Tìm tiệm cận ngang của đồ thị hàm số $y=\frac{x-1}{4x+1}$.
Giải
Tập xác định D = ℝ \ $\{\frac{-1}{4}\}$.
Ta có $\underset{x\rightarrow+\infty}{lim}\frac{x-1}{4x+1}=\frac{1}{4}$.
Vậy đường thẳng $y=\frac{1}{4}$ là một tiệm cận ngang của đồ thị hàm số.
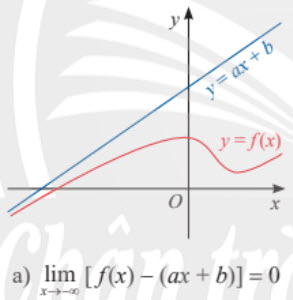
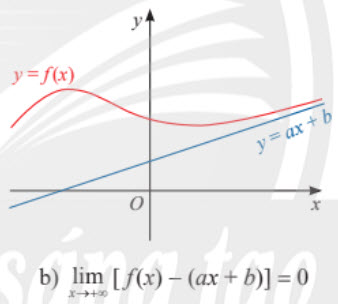
3. Đường tiệm cận xiên
Đường thẳng y = ax + b, a ≠ 0 gọi là một đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu
$\underset{x\rightarrow-\infty}{lim}\;[f(x)-(ax+b)]=0$ hoặc $\underset{x\rightarrow+\infty}{lim}\;[f(x)-(ax+b)]=0$.
Nhận xét:
a) Có thể tìm các hệ số a, b trong phương trình y = ax + b như sau:
$a=\underset{x\rightarrow+\infty}{lim}\frac{f(x)}{x},b=\underset{x\rightarrow+\infty}{lim}\;[f(x)-ax]$
hoặc $a=\underset{x\rightarrow-\infty}{lim}\frac{f(x)}{x},b=\underset{x\rightarrow-\infty}{lim}\;[f(x)-ax]$.
b) Khi a =0 thì đồ thị hàm số có tiệm cận ngang là đường thẳng y = b.
Ví dụ
Tìm tiệm cận xiên của đồ thị hàm số $y=\frac{2x^2-3x}{x+5}$.
Giải
Tập xác định D = ℝ \ {-5}.
Ta có $y=f(x)=\frac{2x^2-3x}{x+5}=2x-13+\frac{65}{x+5}$,
Do đó, $\underset{x\rightarrow-\infty}{lim}\;[f(x)-(2x-13)]=\underset{x\rightarrow-\infty}{lim}\frac{65}{x+5}=0$.
Vậy tiệm cận xiên của đồ thị hàm số là đường thẳng y = 2x - 13.
Xem thêm các bài học khác :