Bài 1. Tính đơn điệu và cực trị của hàm số
Chương I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
1. Tính đơn điệu của hàm số
Cho hàm số y = f(x) có đạo hàm trên K.
Nếu f'(x) > 0 với mọi x thuộc K thì hàm số y = f(x) đồng biến trên K.
Nếu f'(x) < 0 với mọi x thuộc K thì hàm số y = f(x) nghịch biến trên K.
Chú ý:
Có thể f'(x) = 0 tại một số hữu hạn điểm. Nếu f'(x) = 0 với mọi x ∈ K thì hàm số không đổi trên K.
Xét tính đơn điệu của hàm số y = f(x), ta thực hiện các bước sau:
Bước 1: Tìm tập xác định D của hàm số.
Bước 2: Tính đạo hàm f'(x) của hàm số. Tìm các điểm x thuộc D mà tại đó f'(x) = 0 hoặc đạo hàm không tồn tại.
Bước 3: Xét dấu f'(x) và lập bảng biến thiên.
Bước 4: Nếu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Ví dụ
Xét tính đơn điệu của hàm số $g(x)=\frac{1}{x}$.
Giải
Xét hàm số $g(x)=\frac{1}{x}$ có tập xác định D = ℝ \ {0}.
Ta có $g'(x)=\frac{-1}{x^2}$.
Vì x2 > 0 với mọi x ∈ D nên g'(x) < 0 với mọi x ∈ D.
Ta có các giới hạn sau:
$\underset{x\rightarrow+\infty}{lim}g(x)=0;\underset{x\rightarrow-\infty}{lim}g(x)=0;\underset{x\rightarrow0^-}{lim}g(x)=-\infty;\underset{x\rightarrow0^+}{lim}g(x)=+\infty$.
Bảng biến thiên:
Vậy hàm số nghịch biến trên các khoảng (-∞ ; 0) và (0 ; +∞).
2. Cực trị của hàm số
Khái niệm cực trị của hàm số
Cho hàm số y = f(x) xác định trên tập hợp D và x0 ∈ D. Tồn tại một khoảng (a ; b) chứa điểm x0 và (a ; b) ⊂ D.
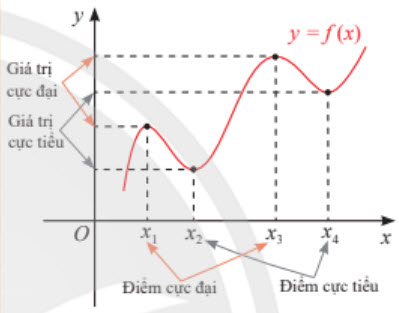
• Nếu f(x) < f(x0) với mọi x ∈ (a ; b) \ {x0} thì x0 gọi là một điểm cực đại của y = f(x), kí hiệu yCĐ.
• Nếu f(x) > f(x0) với mọi x ∈ (a ; b) \ {x0} thì x0 gọi là một điểm cực tiểu của y = f(x), kí hiệu yCT.
Chú ý:
• Điểm cực đại và điểm cực tiểu gọi chung là điểm cực trị của hàm số. Giá trị cực đại và Giá trị cực tiểu gọi chung là giá trị cực trị (hay cực trị) của hàm số.
• Nếu x0 là một điểm cực trị của hàm số y = f(x) (ta cũng nói hàm số y = f(x) đạt cực trị tại x0) thì điểm M(x0 ; f(x0)) là một điểm cực trị của đồ thị hàm số y = f(x). Hàm số có thể đạt cực trị tại nhiều điểm trên D.
Tìm cực trị của hàm số
Cho hàm số y = f(x) liên tục trên khoảng (a ; b) chứa điểm x0 và có đạo hàm trên các khoảng (a ; x0) và (x0 ; b). Khi đó:
• Nếu f'(x) < 0 với mọi x ∈ (a ; x0) và f'(x) > 0 với mọi x ∈ (x0 ; b) thì hàm số y = f(x) đạt cực tiểu tại điểm x0.
• Nếu f'(x) > 0 với mọi x ∈ (a ; x0) và f'(x) < 0 với mọi x ∈ (x0 ; b) thì hàm số y = f(x) đạt cực đại tại điểm x0.
Nhận xét:
Tìm cực trị của hàm số y = f(x), ta thực hiện các bước sau:
Bước 1: Tìm tập xác định D của hàm số.
Bước 2: Tính đạo hàm f'(x) của hàm số. Tìm các điểm x thuộc D mà tại đó f'(x) = 0 hoặc đạo hàm không tồn tại.
Bước 3: Lập bảng biến thiên của hàm số.
Bước 4: Từ bảng biến thiên kết luận về cực trị của hàm số.
Chú ý:
a) Nếu f'(x0) = 0 và f'(x) không đổi dấu khi x qua điểm x0 thì hàm số không đạt cực trị tại x0.
a) Nếu f'(x) không đổi dấu trên khoảng K thì f(x) không có cực trị trên K.
Ví dụ
Tìm cực trị của hàm số $g(x)=\frac{x^2+x+4}{x+1}$.
Giải
Tập xác định D = ℝ \ {-1}.
Ta có $g'(x)=\frac{x^2+2x-3}{(x+1)^2}$.
g'(x) = 0 ⇔ x2 + 2x - 3 = 0 ⇔ x = 1 hoặc x = -3.
Ta có các giới hạn sau:
$\underset{x\rightarrow-\infty}{lim}g(x)=-\infty;\underset{x\rightarrow+\infty}{lim}g(x)=+\infty;\underset{x\rightarrow-1^-}{lim}g(x)=-\infty;\underset{x\rightarrow-1^+}{lim}g(x)=+\infty$.
Bảng biến thiên:
Vậy hàm số đạt cực đại tại x = -3, giá trị cực đại là g(-3) = -5; hàm số đạt cực tiểu tại x = 1, giá trị cực tiểu là g(1) = 3.
Xem thêm các bài học khác :