Bài 2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương
Chương 3. Các hình khối trong thực tiễn
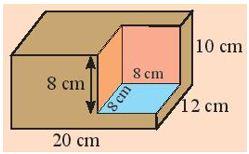
Làm thế nào để tính được tổng diện tích các mặt và thể tích của khối gỗ ở hình bên?
1. Công thức tính diện tích xung quanh và thể tích
Ta kí hiệu Sxq là diện tích xung quanh, V là thể tích.
Hình hộp chữ nhật
Sxq = 2 . (a + b) . h
V = a . b . h = S . h
(S là diện tích đáy).
Hình lập phương
Sxq = 4 . a2
V = a3
Ví dụ
Một khối bê tông, được đặt trên mặt đất, có kích thước như Hình 3.
a) Người ta muốn sơn tất cả các mặt của khối bê tông trừ mặt tiếp giáp với mặt đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.
b) Tính thể tích của khối bê tông.
Giải
Quan sát Hình 3, ta thấy khối bê tông gồm 2 phần là hình hộp chữ nhật thứ 1 (kích thước đáy 4m x 5m, chiều cao 5m) và hình hộp chữ nhật thứ 2 (kích thước đáy 10m x 10m, chiều cao 3m).
a) Diện tích xung quanh của hình hộp chữ nhật thứ 1 là Sxq1 = 2.(4+5).5 = 90 (m2).
Diện tích xung quanh của hình hộp chữ nhật thứ 2 là Sxq2 = 2.(10+10).3 = 120 (m2).
Người ta muốn sơn tất cả các mặt của khối bê tông trừ mặt tiếp giáp với mặt đất, do đó tổng diện tích cần sơn là:
S = Sxq1 + Sxq2 + S1 + S2 . Trong đó:
S1 là diện tích mặt đáy trên của hình hộp chữ nhật thứ 1: S1 = 4.5 = 20 (m2).
S2 là phần diện tích mặt đáy trên không bị che của hình hộp chữ nhật thứ 2: S2 = 10.10 - 4.5 = 80 (m2).
Ta có, S = 90 + 120 + 20 + 80 = 310 (m2).
Vậy chi phí để sơn khối bê tông là 310 . 25 000 = 7 750 000 (đồng).
b) Thể tích của hình hộp chữ nhật thứ 1 là 4.5.5 = 100 (m3).
Thể tích của hình hộp chữ nhật thứ 2 là 10.10.3 = 300 (m3).
Vậy thể tích của khối bê tông là 100 + 300 = 400 (m3).
Xem thêm các bài học khác :