Bài 3. Giải tam giác và ứng dụng thực tế
Chương 4. Hệ thức lượng trong tam giác
1. Giải tam giác
Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó.
Để giải tam giác, ta thường sử dụng một cách hợp lí các hệ thức lượng như: định lí sin, định lí côsin và các công thức tính diện tích tam giác.
Ví dụ
Giải tam giác ABC trong trường hợp sau: a = 17,4; $\widehat{B}$ = 44°30'; $\widehat{C}$ = 64°.
Giải
Ta cần tính hai cạnh b, c và góc A.
• $\widehat{A}=180°-(\widehat{B}+\widehat{C})$ = 180° - (44°30' + 64°) = 71°30'.
• Áp dụng định lí sin ta có:
$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$
⇒ b = $\frac{asinB}{sinA}=\frac{17,4.sin44°30'}{sin71°30'}$ ≈ 12,9; c = $\frac{asinC}{sinA}=\frac{17,4.sin64°}{sin71°30'}$ ≈ 16,5.
2. Ứng dụng giải tam giác thực tế
Vận dụng giải tam giác giúp ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
Ví dụ
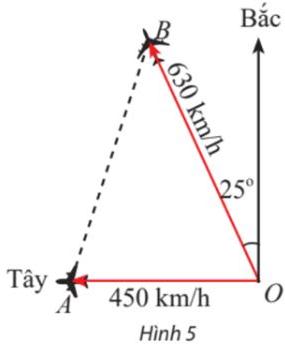
Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với vận tốc 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc 25° về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilômét? Giả sử chúng đang ở cùng độ cao.
Giải
Sau 90 phút (hay 1,5 giờ) hai máy bay đi được quãng đường là:
OA = 450 . 1,5 = 675 (km) và OB = 630 . 1,5 = 945 (km).
• Xét ∆AOB, ta có: $\widehat{AOB}$ = 90° −25° = 65°, theo định lí côsin ta có:
AB2 = OA2 + OB2 – 2.OA.OB.cos O = 6752 + 9452 – 2.675.945.cos65o ≈ 809 495
⇒ AB = $\sqrt{809495}$ ≈ 900 (km).
Vậy sau 90 phút hai máy bay cách nhau khoảng 900 km.
Xem thêm các bài học khác :