Bài 1. Vectơ và các phép toán trong không gian
Chương II. VECTƠ VÀ HỆ TỌA ĐỘ TRONG KHÔNG GIAN
1. Vectơ trong không gian
Ví dụ
Cho hình chóp tứ giác đều S.ABCD.
a) Chỉ ra các vectơ có điểm đầu là S và điểm cuối là các đỉnh của đa giác đáy.
b) Tìm các vectơ có độ dài bằng độ dài của vectơ $\overrightarrow{SA}$.
c) Tìm các vectơ đối của vectơ $\overrightarrow{CB}$.
Giải
Hình chóp tứ giác đều S.ABCD nên có đáy là hình vuông ABCD; các cạnh bên SA, SB, SC, SD bằng nhau.
a) Các vectơ có điểm đầu là S và điểm cuối là các đỉnh của đa giác đáy: $\overrightarrow{SA},\;\overrightarrow{SB},\;\overrightarrow{SC},\;\overrightarrow{SD}$.
b) Ta có SA = SB = SC = SD nên các vectơ có độ dài bằng độ dài của vectơ $\overrightarrow{SA}$ là:
$\overrightarrow{SB},\;\overrightarrow{BS},\;\overrightarrow{SC},\;\overrightarrow{CS},\;\overrightarrow{SD},\;\overrightarrow{DS}$.
c) Xét hình vuông ABCD, hai vectơ $\overrightarrow{CB}$ và $\overrightarrow{AD}$ ngược hướng và có độ dài bằng nhau nên $\overrightarrow{AD}$ là vectơ đối của $\overrightarrow{CB}$.
Hai vectơ $\overrightarrow{CB}$ và $\overrightarrow{BC}$ ngược hướng và có độ dài bằng nhau nên $\overrightarrow{BC}$ là vectơ đối của $\overrightarrow{CB}$.
Vậy các vectơ đối của $\overrightarrow{CB}$ là $\overrightarrow{AD},\;\overrightarrow{BC}$.
2. Tổng và hiệu của hai vectơ
Tổng của hai vectơ
Trong không gian, cho hai vectơ $\overrightarrow{a},\;\overrightarrow{b}$. Lấy điểm O bất kì và hai điểm A, B sao cho $\overrightarrow{OA}=\overrightarrow{a},\;\overrightarrow{AB}=\overrightarrow{b}$. Ta gọi $\overrightarrow{OB}$ là tổng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu ${\color{Blue}\overrightarrow{a}+\overrightarrow{b}}$.
Phép lấy tổng của hai vectơ gọi là phép cộng vectơ. (Hình 6)
Nhận xét: Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng.
• Tính chất giao hoán: ${\color{Blue}\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}}$;
• Tính chất kết hợp: ${\color{Blue}\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)}$;
• Với mọi vectơ $\overrightarrow{a}$, ta luôn có: ${\color{Blue}\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}}$.
Chú ý: Từ tính chất kết hợp, ta có ${\color{Blue}\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}}$.
Quy tắc ba điểm (Hình 7a), quy tắc hình bình hành (Hình 7b) vẫn đúng với các vectơ trong không gian.
• Với ba điểm A, B, C ta có ${\color{Blue}\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}}$.
• ABCD là hình bình hành thì ta có ${\color{Blue}\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}}$.
Quy tắc hình hộp
Cho hình hộp ABCD.A'B'C'D'. Ta có ${\color{Blue}\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}}$. (Hình 10)
Hiệu của hai vectơ
Trong không gian, cho hai vectơ $\overrightarrow{a},\;\overrightarrow{b}$. Ta gọi ${\color{Blue}\overrightarrow{a}+(\overrightarrow{-b})}$ là hiệu của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu ${\color{Blue}\overrightarrow{a}-\overrightarrow{b}}$.
Phép lấy hiệu của hai vectơ gọi là phép trừ vectơ.
Quy tắc hiệu
Trong không gian, với ba điểm A, B, C ta có ${\color{Blue}\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}}$. (Hình 15)
Ví dụ
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Tìm các vectơ:
a) $\overrightarrow{BM}+\overrightarrow{AC}+\overrightarrow{ND}$;
b) $\overrightarrow{AD}-\overrightarrow{AM}+\overrightarrow{NC}$.
Giải
a) M là trung điểm của AB nên $\overrightarrow{BM}=\overrightarrow{MA}$,
N là trung điểm của DC nên $\overrightarrow{ND}=\overrightarrow{CN}$, suy ra
$\overrightarrow{BM}+\overrightarrow{AC}+\overrightarrow{ND}=\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{CN}$ =
= $\overrightarrow{MC}+\overrightarrow{CN}=\overrightarrow{MN}$.
b) N là trung điểm của DC nên $\overrightarrow{NC}=\overrightarrow{DN}$, suy ra
$\overrightarrow{AD}-\overrightarrow{AM}+\overrightarrow{NC}=\overrightarrow{MD}+\overrightarrow{NC}$ =
= $\overrightarrow{MD}+\overrightarrow{DN}=\overrightarrow{MN}$.
3. Tích của một số với một vectơ
Trong không gian, cho số thực k ≠ 0 và vectơ $\overrightarrow{a}\neq\overrightarrow{0}$.
Tích của số k với vectơ $\overrightarrow{a}$ là một vectơ, kí hiệu ${\color{Blue}k\overrightarrow{a}}$, cùng hướng với $\overrightarrow{a}$ nếu k > 0, ngược hướng với $\overrightarrow{a}$ nếu k < 0 và có độ dài bằng ${\color{Blue}|k|.|\overrightarrow{a}|}$.
Phép lấy tích của một số với một vectơ goi là phép nhân một số với một vectơ.
Quy ước: ${\color{Blue}0.\overrightarrow{a}=\overrightarrow{0}}$ và ${\color{Blue}k.\overrightarrow{0}=\overrightarrow{0}}$.
Nhận xét:
a) Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bất kì, với mọi số h và k, ta có:
• ${\color{Blue}k\left(\overrightarrow{a}+\overrightarrow{b}\right)=k\overrightarrow{a}+k\overrightarrow{b}}$;
• ${\color{Blue}(h+k)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a}}$;
• ${\color{Blue}h(k\overrightarrow{a})=(hk)\overrightarrow{a}}$;
• ${\color{Blue}1.\overrightarrow{a}=\overrightarrow{a}}$;
• ${\color{Blue}(-1).\overrightarrow{a}=-\overrightarrow{a}}$.
b) ${\color{Blue}k.\overrightarrow{a}=\overrightarrow{0}}$ ⇔ ${\color{Blue}\overrightarrow{a}=\overrightarrow{0}}$ hoặc k = 0.
c) Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}\;\left(\overrightarrow{b}\neq\overrightarrow{0}\right)$ cùng phương khi và chỉ khi có số k sao cho ${\color{Blue}\overrightarrow{a}=k\overrightarrow{b}}$.
d) Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để ${\color{Blue}\overrightarrow{AB}=k\overrightarrow{AC}}$.
Ví dụ
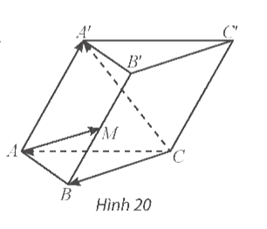
Cho hình lăng trụ ABC.A'B'C' có M là trung điểm của BB' (Hình 20). Đặt $\overrightarrow{CA}=\overrightarrow{a},\overrightarrow{CB}=\overrightarrow{b},\overrightarrow{CC'}=\overrightarrow{c}$.
Chứng minh rằng $\overrightarrow{AM}=\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{c}$.
Giải
ABC.A'B'C' là hình lăng trụ nên $\overrightarrow{CC'}=\overrightarrow{BB'}$,
M là trung điểm của BB' nên $\frac{1}{2}\overrightarrow{BB'}=\overrightarrow{BM}$,
do đó, $\frac{1}{2}\overrightarrow{CC'}=\overrightarrow{BM}$ suy ra
$\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{c}=\overrightarrow{CB}-\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CC'}$ =
= $\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AM}$.
Vậy $\overrightarrow{AM}=\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{c}$.
4. Tích vô hướng của hai vectơ
Góc giữa hai vectơ trong không gian
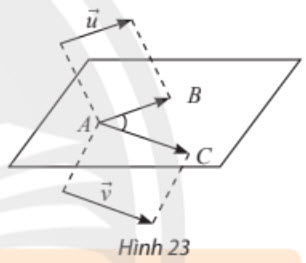
Trong không gian, cho $\overrightarrow{u}$ và $\overrightarrow{v}$ là hai vectơ khác vectơ $\overrightarrow{0}$. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho $\overrightarrow{AB}=\overrightarrow{u},\;\overrightarrow{AC}=\overrightarrow{v}$. Khi đó, ta gọi ${\color{Blue}\widehat{BAC}}$ là góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$, kí hiệu ${\color{Blue}\left(\overrightarrow{a},\;\overrightarrow{b}\right)}$. (Hình 23)
Nhận xét:
• 0° ≤ $\left(\overrightarrow{a},\;\overrightarrow{b}\right)$ ≤ 180°;
• Nếu $\left(\overrightarrow{a},\;\overrightarrow{b}\right)$ = 90° thì ta nói $\overrightarrow{u}$ và $\overrightarrow{v}$, kí hiệu ${\color{Blue}\overrightarrow{u}\bot\overrightarrow{v}}$.
Tích vô hướng của hai vectơ
Trong không gian, cho hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ khác $\overrightarrow{0}$.
Tích vô hướng của hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ là một số, kí hiệu ${\color{Blue}\overrightarrow{u}.\overrightarrow{v}}$, được xác định bởi công thức
${\color{Blue}\overrightarrow{u}.\overrightarrow{v}=|\overrightarrow{u}|.|\overrightarrow{v}|.cos(\overrightarrow{u},\overrightarrow{v})}$.
Chú ý:
a) $\overrightarrow{u}=\overrightarrow{0}$ hoặc $\overrightarrow{v}=\overrightarrow{0}$, ta quy ước ${\color{Blue}\overrightarrow{u}.\overrightarrow{v}=0}$.
b) • ${\color{Blue}\overrightarrow{u}.\overrightarrow{u}=\overrightarrow{u}^2=\left|\overrightarrow{u}\right|^2}$;
• ${\color{Blue}\overrightarrow{u}^2\geq0,\overrightarrow{u}^2=0\Leftrightarrow\overrightarrow{u}=\overrightarrow{0}}$.
c) Với $\overrightarrow{u}$ và $\overrightarrow{v}$ khác $\overrightarrow{0}$, ta có:
• ${\color{Blue}\cos(\overrightarrow{u},\overrightarrow{v})=\frac{\overrightarrow{u}.\overrightarrow{v}}{|\overrightarrow{u}|.|\overrightarrow{v}|}}$;
• ${\color{Blue}\overrightarrow{u}\bot\overrightarrow{v}\Leftrightarrow\overrightarrow{u}.\overrightarrow{v}=0}$.
Nhận xét:
Trong không gian, với ba vectơ $\overrightarrow{a},\;\overrightarrow{b},\;\overrightarrow{c}$ và số k, ta có:
• ${\color{Blue}\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}}$;
• ${\color{Blue}\overrightarrow{a}.\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}}$;
• ${\color{Blue}(k\overrightarrow{a}).\overrightarrow{b}=k(\overrightarrow{a}.\overrightarrow{b})=\overrightarrow{a}.(k\overrightarrow{b})}$.
Ví dụ
1) Cho hình lập phương ABCD.A'B'C'D'. Xác định góc $\left(\overrightarrow{AC},\;\overrightarrow{B'D'}\right),\;\left(\overrightarrow{A'A},\;\overrightarrow{CB'}\right)$.
Giải
• Ta có $\overrightarrow{B'D'}=\overrightarrow{BD}$ và AC ⊥ BD nên $\left(\overrightarrow{AC},\;\overrightarrow{B'D'}\right)=\left(\overrightarrow{AC},\;\overrightarrow{BD}\right)$ = 90°.
• Lấy M ∈ CC' sao cho $\overrightarrow{A'A}=\overrightarrow{CM}$.
Ta có $\left(\overrightarrow{A'A},\;\overrightarrow{CB'}\right)=\left(\overrightarrow{CM},\;\overrightarrow{CB'}\right)$ =
= $\widehat{MCB'}=180^o-\widehat{C'CB'}$ = 180° - 45° = 135°.
2) Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính các tích vô hướng: $\overrightarrow{AB}.\overrightarrow{A'C'},\;\overrightarrow{AB}.\overrightarrow{CC'}$.
Giải
• $\left(\overrightarrow{AB},\;\overrightarrow{A'C'}\right)=\left(\overrightarrow{AB},\;\overrightarrow{AC}\right)=\widehat{BAC}$ = 45°,
ta có $\overrightarrow{AB}.\overrightarrow{A'C'}=|\overrightarrow{AB}|.|\overrightarrow{A'C'}|.cos(\overrightarrow{AB},\overrightarrow{A'C'})$ =
= AB.A'C'.cos45° = 1.$\sqrt{2}.\frac{\sqrt{2}}{2}$ = 1.
(A'B'C'D' là hình vuông cạnh bằng 1 nên A′C′ = $\sqrt{2}$.)
• CC' ⊥ AB (vì CC' ⊥ mp(ABCD) ) ⇒ $\overrightarrow{AB}\bot\overrightarrow{CC'}$, do đó $\overrightarrow{AB}.\overrightarrow{CC'}$ = 0.
Xem thêm các bài học khác :