Bài 2. Hàm số bậc hai
Chương 3. Hàm số bậc hai và đồ thị
1. Hàm số bậc hai
Ví dụ
Cho các hàm số:
a) y = 2x(x – 3); b) y = x(x2 + 2) – 5; c) y = -5(x + 1)(x – 4).
Hàm số nào là hàm số bậc hai?
Giải
Hàm số bậc hai y = f(x) có dạng: y = ax2 + bx + c (với a ≠ 0).
a) y = 2x(x – 3) = 2x2 – 6x là hàm số bậc hai (với a = 2, b = -6, c = 0).
b) y = x(x2 + 2) – 5 = x3 + 2x – 5 không phải là hàm số bậc hai.
c) y = -5(x + 1)(x – 4) = -5x2 + 15x + 20 là hàm số bậc hai (với a = -5, b = 15, c = 20).
2. Đồ thị hàm số bậc hai
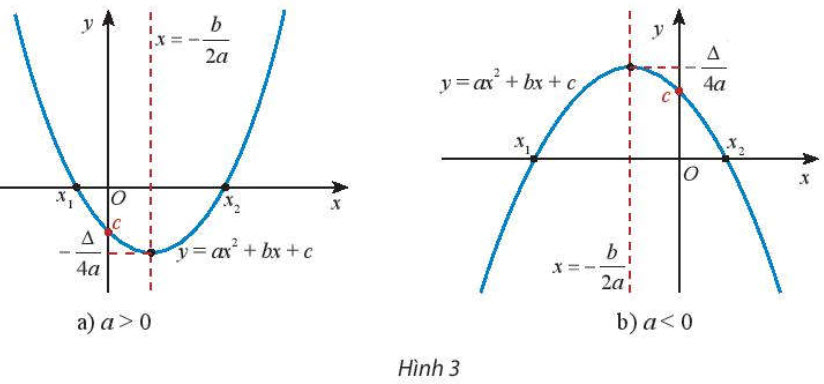
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) là một parabol (P):
• Có tọa độ đỉnh S là ${\color{Blue}\left(\frac{-b}{2a};\frac{-∆}{4a}\right)}$;
• Có trục đối xứng là đường thẳng ${\color{Blue}x=\frac{-b}{2a}}$;
• Có bề lõm quay lên trên nếu a > 0, quay xuống dưới nếu a < 0;
• Cắt trục tung tại điểm có tọa độ (0 ; c).
• Nếu ax2 + bx + c = 0 có hai nghiệm x1, x2 thì (P) cắt trục hoành tại hai điểm (x1 ; 0) và (x2 ; 0) (xem Hình 3).
Ví dụ
Vẽ đồ thị hàm số y = x2 – 4x + 3.
Giải
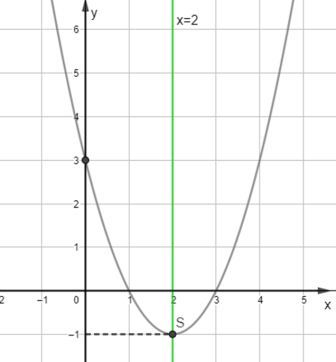
Đồ thị của y = x2 – 4x + 3 là một parabol (P):
• Có đỉnh S(2 ; -1);
• Có trục đối xứng là đường thẳng x = 2;
• Cắt trục tung tại điểm (0; 3); cắt trục hoành tại hai điểm (1 ; 0) và (3 ; 0).
3. Sự biến thiên của hàm số bậc hai
Dựa vào đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0), ta có bảng tóm tắt về sự biến thiên của hàm số này như sau:
a > 0
Hàm số nghịch biến trên khoảng $\left(-∞;\frac{-b}{2a}\right)$ và đồng biến trên khoảng $\left(\frac{-b}{2a};+∞\right)$.
Bảng biến thiên:
a < 0
Hàm số đồng biến trên khoảng $\left(-∞;\frac{-b}{2a}\right)$ và nghịch biến trên khoảng $\left(\frac{-b}{2a};+∞\right)$.
Bảng biến thiên:
Chú ý: Từ bảng biến thiên của hàm số bậc hai, ta thấy:
• Khi a > 0, hàm số đạt giá trị nhỏ nhất bằng ${\color{Blue}\frac{-∆}{4a}}$ tại $x=\frac{-b}{2a}$ và hàm số có tập giá trị là T = [ $\frac{-∆}{4a}$ ; +∞ ).
• Khi a < 0, hàm số đạt giá trị lớn nhất bằng ${\color{Blue}\frac{-∆}{4a}}$ tại $x=\frac{-b}{2a}$ và hàm số có tập giá trị là T = ( -∞ ; $\frac{-∆}{4a}$ ].
Ví dụ
Tìm khoảng đồng biến, khoảng nghịch biến của hàm số y = 2x2 – 6x + 11. Hàm số có thể đạt giá trị bằng -1 không? Tại sao?
Giải
Đồ thị hàm số y = 2x2 – 6x + 11 (với a = 2 > 0) có tọa độ đỉnh $S\left(\frac{3}{2};\frac{13}{2}\right)$.
Do đó, hàm số nghịch biến trên khoảng (-∞ ; $\frac{3}{2}$) và đồng biến trên khoảng ($\frac{3}{2}$ ; +∞).
Hàm số đạt giá trị nhỏ nhất là $\frac{13}{2}$ tại x = $\frac{3}{2}$ (hay y ≥ $\frac{13}{2}$) nên hàm số không thể đạt giá trị bằng -1.
Xem thêm các bài học khác :