Bài 1. Hàm số và đồ thị
Chương 3. Hàm số bậc hai và đồ thị
1. Hàm số. Tập xác định và tập giá trị của hàm số
♦ Cho x, y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số D.
Nếu với mỗi giá trị x ∈ D, ta xác định được một và chỉ một giá trị tương ứng y ∈ ℝ thì ta có một hàm số.
Ta gọi x là biến số và y là hàm số của x.
Tập hợp D được gọi là tập xác định của hàm số.
Tập hợp T gồm tất cả các giá trị y (tương ứng với x ∈ D) gọi là tập xác định của hàm số.
Ta thường dùng kí hiệu f(x) để chỉ giá trị y tương ứng với x, nên hàm số còn được viết là y = f(x).
♦ Một hàm số có thể được cho bằng bảng (như Bảng 1), bằng biểu đồ (như Hình 1) hoặc bằng công thức (chẳng hạn y = 2x - 3, y = -x2).
| Giờ | 1 | 4 | 7 | 10 | 13 | 16 | 19 | 22 |
|---|---|---|---|---|---|---|---|---|
| Nhiệt độ (°C) | 28 | 27 | 28 | 32 | 31 | 29 | 28 | 27 |
Chú ý:
• Khi hàm số được cho bằng công thức mà không chỉ rõ tập xác định thì ta quy ước:
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
• Một hàm số có thể được cho bởi hai hoặc nhiều công thức. Chẳng hạn xét hàm số:
$f(x)=\left\{\begin{matrix}-3x+5 với x≤1\\2x^2 với x>1\end{matrix}\right.$
nghĩa là với x ≤ 1 thì f(x) = -3x + 5; với x > 1 thì f(x) = 2x2.
Ví dụ
1) Một thiết bị đã ghi lại vận tốc v (m/s) ở thời điểm t (s) của một vật chuyển động như trong bảng sau:
t (s)
0,5
1
1,2
1,8
2,5
v (m/s)
1,5
3
0
5,4
7,5
Vì sao bảng này biểu thị một hàm số? Tìm tập xác định của hàm số này.
Giải
Bảng này biểu thị một hàm số vì từ bảng ta thấy ứng với mỗi thời điểm t (s) đều chỉ có một giá trị vận tốc v (m/s). Do đó, vận tốc v (m/s) là hàm số của biến thời điểm t (s).
Tập xác định D của hàm số là: D = {0,5; 1; 1,2; 1,8; 2,5}.
2) Tìm tập xác định của các hàm số sau:
a) f(x) = $\sqrt{2x+7}$; b) f(x) = $\frac{x+4}{x^2-3x+2}$.
Giải
a) f(x) có nghĩa khi 2x + 7 ≥ 0 ⇔ x ≥ $\frac{-7}{2}$.
Vậy tập xác định của hàm số là D = [ $\frac{-7}{2}$ ; +∞).
b) f(x) có nghĩa khi x2−3x+2 ≠ 0 ⇔ x ≠ 1 và x ≠ 2.
Vậy tập xác định của hàm số là D = ℝ \ {1; 2}.
2. Đồ thị hàm số
3. Hàm số đồng biến, hàm số nghịch
Ví dụ
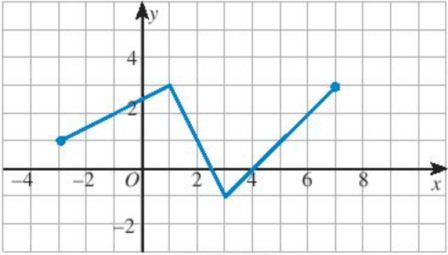
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b) Xét tính đồng biến, nghịch biến của hàm số y = f(x) = 5x2 trên khoảng (2 ; 5).
Giải
a) Quan sát đồ thị hàm số, ta thấy:
• Tập xác định của hàm số là D = [-3; 7].
• Hàm số đồng biến trên các khoảng (-3 ; 1) và (3 ; 7) (vì đồ thị hàm số đi lên từ trái sang phải).
• Hàm số nghịch biến trên khoảng (1 ; 3) (vì đồ thị hàm số đi xuống từ trái sang phải).
b) Lấy x1, x2 ∈ (2; 5) với x1 < x2, ta có:
f(x1) – f(x2) = 5x12 – 5x22 = 5(x12 – x22) = 5(x1 – x2)(x1 + x2).
x1, x2 ∈ (2 ; 5) ⇒ x1 + x2 > 0 (1)
x1 < x2 ⇒ x1 – x2 < 0 (2)
Từ (1) và (2) suy ra f(x1) – f(x2) = 5(x1 – x2)(x1 + x2) < 0 ⇔ f(x1) < f(x2).
Vậy hàm số y = 5x2 đồng biến trên khoảng (2 ; 5).
Xem thêm các bài học khác :